Пусть 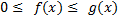 на интервале
на интервале 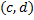 . Тогда
. Тогда
1) если  сходится, то
сходится, то  сходится;
сходится;
2) если  расходится, то
расходится, то  расходится.
расходится.
Доказательство. 1) Если  сходится, то существует (конечная) площадь криволинейной трапеции Т под графиком функции
сходится, то существует (конечная) площадь криволинейной трапеции Т под графиком функции  . Криволинейная трапеция под графиком функции
. Криволинейная трапеция под графиком функции 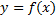 содержится в Т, следовательно и у нее площадь также конечна. Тем самым интеграл
содержится в Т, следовательно и у нее площадь также конечна. Тем самым интеграл  сходится.
сходится.
2) следует из 1) в силу логического принципа: импликация 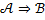 эквивалентна импликации
эквивалентна импликации  (черта сверху – отрицание утверждения). Более подробно: если бы интеграл
(черта сверху – отрицание утверждения). Более подробно: если бы интеграл  сходился, то и интеграл
сходился, то и интеграл  также бы сходился, согласно первому утверждению. Это, однако, противоречит условию. Противоречие показывает, что интеграл
также бы сходился, согласно первому утверждению. Это, однако, противоречит условию. Противоречие показывает, что интеграл  должен расходится. □
должен расходится. □
Следствие. Пусть функции  кусочно непрерывны и имеют неотрицательные значения на полуинтервале
кусочно непрерывны и имеют неотрицательные значения на полуинтервале 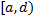 . Предположим, что существует предел
. Предположим, что существует предел 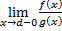 причём он отличен от 0. Тогда интегралы
причём он отличен от 0. Тогда интегралы  и
и  ведут себя одинаково в смысле сходимости, т.е. либо оба сходятся, либо оба расходятся.
ведут себя одинаково в смысле сходимости, т.е. либо оба сходятся, либо оба расходятся.
Аналогичное утверждение имеет место для полуинтервала (c,b].
Предложение об "эталонных" интегралах. Пусть a>0.
1. Интеграл  сходится тогда и только тогда, когда p>1.
сходится тогда и только тогда, когда p>1.
2. Интеграл  сходится тогда и только тогда, когда p<1.
сходится тогда и только тогда, когда p<1.
Доказательство. 1. Если 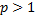 , то первообразная
, то первообразная  подинтегральной функции
подинтегральной функции  имеет конечный предел 0 при
имеет конечный предел 0 при 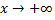 . По формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интеграл
. По формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интеграл  сходится и равен
сходится и равен  .
.
Если 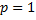 , то первообразной подинтегральной функции служит
, то первообразной подинтегральной функции служит  , который не имеет конечного предела на
, который не имеет конечного предела на  . Для
. Для 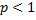 то же самое можно сказать о первообразной
то же самое можно сказать о первообразной 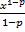 .
.
Аналогично, прямыми вычислениями доказывает второе утверждение.

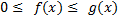 на интервале
на интервале 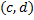 . Тогда
. Тогда сходится, то
сходится, то  сходится;
сходится; расходится, то
расходится, то  . Криволинейная трапеция под графиком функции
. Криволинейная трапеция под графиком функции 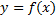 содержится в Т, следовательно и у нее площадь также конечна. Тем самым интеграл
содержится в Т, следовательно и у нее площадь также конечна. Тем самым интеграл 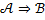 эквивалентна импликации
эквивалентна импликации  (черта сверху – отрицание утверждения). Более подробно: если бы интеграл
(черта сверху – отрицание утверждения). Более подробно: если бы интеграл  кусочно непрерывны и имеют неотрицательные значения на полуинтервале
кусочно непрерывны и имеют неотрицательные значения на полуинтервале 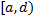 . Предположим, что существует предел
. Предположим, что существует предел 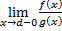 причём он отличен от 0. Тогда интегралы
причём он отличен от 0. Тогда интегралы  и
и  ведут себя одинаково в смысле сходимости, т.е. либо оба сходятся, либо оба расходятся.
ведут себя одинаково в смысле сходимости, т.е. либо оба сходятся, либо оба расходятся. сходится тогда и только тогда, когда p>1.
сходится тогда и только тогда, когда p>1. сходится тогда и только тогда, когда p<1.
сходится тогда и только тогда, когда p<1.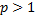 , то первообразная
, то первообразная  подинтегральной функции
подинтегральной функции  имеет конечный предел 0 при
имеет конечный предел 0 при 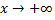 . По формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интеграл
. По формуле Ньютона-Лейбница для несобственных интегралов, получаем, что интеграл  .
.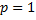 , то первообразной подинтегральной функции служит
, то первообразной подинтегральной функции служит  , который не имеет конечного предела на
, который не имеет конечного предела на  . Для
. Для 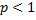 то же самое можно сказать о первообразной
то же самое можно сказать о первообразной 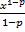 .
.


