Решение. Вначале составим ряды распределения случайных величин X и Y
Вначале составим ряды распределения случайных величин X и Y. Случайная величина X принимает значения –1; 0 и 1 с вероятностями 0,2=0+0,2; 0,3=0,1+0,2 и 0,5=0,4+0,1 соответственно. Таким образом, эта случайная величина имеет закон распределения
Аналогично получаем закон распределения случайной величины Y:
Вероятность P{X<Y}= P{(X= -1),(Y=0)}+P{(X= -1),(Y=1)}+P{(X=0),(Y=1)}= =0+0,2+0,2=0,4. Двумерная величина (ξ, ή) называется непрерывной, если существует такая непрерывная неотрицательная функция f(x,y) двух переменных, что вероятность того, что точка М(ξ, ή) содержится в некоторой области σ плоскости 0ξή;, равна двойному интегралу от функции f(x,y) по области σ:
Плотностью совместного распределения вероятностей (двумерной плотностью вероятности) непрерывной двумерной случайной величины называется смешанная частная производная 2-го порядка от функции распределения:
Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δ х и Δ у к площади этого прямоугольника при Δ х → 0, Δ у →0. Если известна плотность распределения, то функция распределения может быть легко найдена по формуле: Двумерная плотность распределения неотрицательна и двойной интеграл с бесконечными пределами от двумерной плотности должен быть равен единице:
По известной плотности совместного распределения можно найти плотности распределения каждой из составляющих двумерной случайной величины:
Таким образом, зная совместный закон распределения, можно найти законы распределения каждой случайной величины, входящей в систему. Но на практике чаще встречается обратная задача – найти совместный закон распределения по известным законам распределения случайных величин. В общем случае эта задача является неразрешимой, так как закон распределения случайной величины ничего не говорит о связи этой величины с другими случайными величинами. Кроме того, если случайные величины зависимы между собой, то закон распределения не может быть выражен через законы распределения составляющих, т.к. должен устанавливать связь между составляющими. Все это приводит к необходимости рассмотрения условных законов распределения. Условным законом распределения называется распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина приняла определенное значение. Условный закон распределения можно задавать как функцией распределения так и плотностью распределения. Условная плотность распределения вычисляется по формулам:
Условная плотность распределения обладает всеми свойствами плотности распределения одной случайной величины. Условным математическим ожиданием дискретной случайной величины Y при X = x (х – определенное возможное значение Х) называется произведение всех возможных значений Y на их условные вероятности:
Для непрерывных случайных величин: Пример. Найти условное математическое ожидание составляющей Y при X=x1=1 для дискретной двумерной случайной величины, заданной таблицей:
|
.
.
.
.
, 
,
,
.
, 
.
.
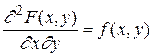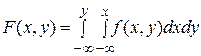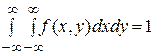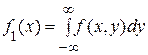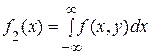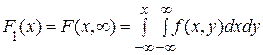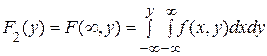, где f(y/x) – условная плотность случайной величины Y при X=x. Условное математическое ожидание M(Y/X=x)=f(x) является функцией от х и называется функцией регрессии Х на Y.
