Статистические гипотезы
При статистическом анализе в технике, экономике, социологии для выявления какого-либо факта часто прибегают к выдвижению гипотез (умозаключений) и последующей их проверке. Статистическими гипотезами называют предположения относительно вида распределения случайной величины или его отдельных параметров. Так, например, гипотеза о нормальном законе распределения производительности труда рабочих, гипотеза о равенстве средних размеров деталей, производимых на одинаковых по техническим свойствам станках и т.д. Сопоставление выдвигаемой гипотезы относительно генеральной совокупности, осуществляемое на основании анализа выборки, называется проверкой статистической гипотезы. Статистические гипотезы можно классифицировать как гипотезы о законах распределения и гипотезы о параметрах распределения. Виды задач, решаемых с помощью гипотез, делятся на 4 группы: § способы проверки случайности, независимости и однородности результатов измерений, § задачи по проверке средних значений и дисперсий для одной или двух нормально распределенных случайных величин; § задачи по проверке гипотез о наличии линейной и множественной корреляции и регрессии, § задачи по проверке законов распределения, определения резко выделяющихся результатов, определения вероятности для нахождения генеральных совокупностей. Любая статистическая гипотеза проверяется на основе статистического критерия - формулы (правила) с помощью которого определяется мера расхождения результатов выборочного наблюдения с высказанной гипотезой. В результате этой проверки выдвигаемая гипотеза либо отвергается, либо принимается. Статистических гипотез всегда две и они взаимоисключающие. Выдвигаемую на проверку гипотезу называют нулевой (Н0), противоположную ей гипотезу называют конкурирующей, альтернативной (Н1). Пусть проводится исследование игральной кости – проверяется ее симметричность. Ясно, что в качестве нулевой гипотезы надо считать предположение о полной симметрии кости. Ведь если Н0 верна, то вероятности выпадения всех шести цифр на гранях будут одинаковы – по 1/6. А вот выдвижение в качестве нулевой гипотезы предположения об асимметрии кости ничего бы не дало – в этом случае ничего нельзя сказать о вероятностях выпадения цифр. Выбор критерия для проверки статистических гипотез производят на основании различных принципов. В основном используется принцип отношения правдоподобия. Суть его сводится к выбору такого критерия (К), чтобы при заданном уровне значимости α;, можно было найти критическую точку Ккр, которая разделила бы область значений на 2 части на более или менее правдоподобные в отношении нулевой гипотезы Н0. К сожалению, не существует единого, универсального критерия значимости – их приходится разрабатывать в теории и использовать на практике применительно к особенностям конкретных задач. В результате применения критерия возможны 4 случая: § гипотеза Н0 верна и она принимается согласно критерию, § гипотеза Н0 не верна и она отвергается согласно критерию, § гипотеза Н0 верна, но отвергается (ошибка первого рода), § гипотеза Н0 не верна, но она принимается (ошибка второго рода). С процедурами проверки статистических гипотез связано понятие уровня значимости результатов наблюдений. Уровнем значимости α; называется вероятность совершить ошибку I-го рода, т.е. отвергнуть верную гипотезу. Вероятность совершить ошибку II-го рода, то есть принять неверную гипотезу - обозначается β;. С уменьшением α возрастает вероятность ошибки β;. Мощностью критерия называется выражение (1-β;) - вероятность того, что нулевая гипотеза (Н0) будет отвергнута, если верна конкурирующая (Н1), т.е. вероятность не допустить ошибку II-го рода. При расчетах принято задавать вероятность ошибки I-го рода (уровень значимости α;). Для этого используют следующие значения: 0.1; 0.05; 0.025; 0.01; 0.001; 0.005. Множество значений критерия К разбивается на 2 части, при этом одна из них содержит значения при которых нулевая гипотеза отвергается, а другая - принимается. Критической называется область значений, при которых нулевая гипотеза отвергается. Областью принятия гипотезы является совокупность значений критерия при которых нулевая гипотеза принимается. Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области (т.е. области, где нулевая гипотеза отвергается). Правосторонней называется критическая область (нулевая гипотеза отвергается), если К > Ккр. Левосторонней называется критическая область, если К < Ккр. Двусторонней называется критическая область, которая определяется следующими неравенствами: К < К1кр; К > К2кр.. Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку. Пример. Предположим, что если верна гипотеза Решение. В первом случае границу правосторонней критической области найдем из условия
поэтому Значит,
Поэтому границы правосторонней критической области Чтобы вычислить ошибку второго рода
и мощность критерия Во втором случае правая граница критической области
Поэтому
Значит,
Поэтому мощность критерия во втором случае равна На основе вышеизложенного сформулируем основные этапы проверки статистической гипотезы: 1. Выдвигается нулевая гипотеза Н0 (т.е. предположение, нуждающееся в проверке) и альтернативная гипотеза Н1. 2. Задается величина уровня значимости α;. 3. Задается некоторая функция от результатов наблюдения - (критическая статистика, которая сама является случайной величиной). В предположении о справедливости гипотезы Н0 эта функция подчиняется некоторому хорошо изученному закону распределения и обычно задается в форме таблицы. 4. Из таблицы находят · область неправдоподобно малых значений, · область вероятностных значений, · область неправдоподобно больших значений. Рассмотрим более подробно задачу проверки гипотез о законе распределения, так как во многих практических задачах возникает необходимость определения закона распределения исследуемой случайной величины, проверка согласованности теоретических и эмпирических функций распределения. В этом случае, прежде ставится нулевая гипотеза H0 о том, что случайная величина подчиняется конкретному теоретическому закону распределения F(х). Выдвинутая для проверки гипотеза проверяется по выборке из генеральной совокупности. Предварительно по выборке строится эмпирическая функция распределения исследуемой величины. Затем производится сравнение эмпирического и теоретического распределения с помощью специально подобранных, так называемых, критериев согласия. Различают несколько критериев согласия: χ; 2 Пирсона, Колмогорова, Смирнова и др. Наиболее часто употребляется критерий согласия χ; 2 Пирсона (хи-квадрат). Критерий χ; 2 (хи квадрат - критерий К.Пирсона). Правило применения критерия χ; 2 сводится к следующему алгоритму: 1) рассчитывается значение χ; 2, 2) выбирается уровень значимости критерия 3) по таблице распределения функции Лапласа определяется χ2(k, Согласно критерию χ; 2
Распределение χ; 2 зависит от числа степеней свободы. При применении критерия Пирсона оно равно Критерий имеет ряд ограничений. Он применим для рядов, имеющих большой объем выборки, достаточную величину частот в крайних интервалах (количество интервалов должно быть не менее пяти). Критерий Колмогорова. В качестве меры расхождения между теоретическим и статистическим распределением рассматривается максимальное значение модуля разности между статистической и соответствующей ей теоретической функцией распределения. В качества критерия берется следующее выражение
Алгоритм критерия Колмогорова применяется следующим образом: 1. строится статистическая функция распределения F*(х) и предполагаемая теоретическая функция распределения F(x), 2. определяется максимальная величина Dn модуля разности между этими распределениями, 3. определяется величина Рассуждая аналогичным образом, можно получить статистики и для других задач проверки гипотез (см. таблицу 5.1). Таблица 5.1. Статистики для задач проверки гипотез.
Пример. По результатам п = 9 замеров установлено, что среднее время изготовления детали а) можно ли принять 50с в качестве нормативного времени (математического ожидания) изготовления детали, б) можно ли принять за норматив 49с. Решение. Э та задача о проверке гипотезы о числовом значении математического ожидания при известной дисперсии. а) По условию задачи нулевая гипотеза б) Здесь нулевая гипотеза Пример. Хронометраж затрат времени на сборку узла машины п= 21 слесарей показал, что Решение. Эта задача о проверке гипотезы о числовом значении математического ожидания при неизвестной дисперсии. В качестве основной гипотезы принимается
Вычисляем Пример. По результатам n=4 измерений температуры в печи найдено Решение. m1>m0 Þ выберем правостороннюю критическую область.
Так как используем правостороннюю критическую область и tкр>tнабл, то на данном уровне значимости нулевая гипотеза не отвергается (|tкр|-|tнабл|=0,98). Пример. На основании n = 15 измерений найдено, что средняя высота сальниковой камеры равна Решение.
Вывод:
|

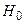 , то критерий
, то критерий 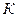 распределен по нормальному закону N (5,3) (т.е. математическое ожидание
распределен по нормальному закону N (5,3) (т.е. математическое ожидание 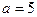 , дисперсия
, дисперсия 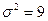 ), а если верна конкурирующая гипотеза
), а если верна конкурирующая гипотеза 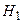 , то критерий распределен по закону N (15,3). Требуется вычислить мощность критерия, когда в качестве критической рассматривается область больших значений, и мощность, когда в качестве критической рассматривается область больших по модулю значений. Уровень значимости
, то критерий распределен по закону N (15,3). Требуется вычислить мощность критерия, когда в качестве критической рассматривается область больших значений, и мощность, когда в качестве критической рассматривается область больших по модулю значений. Уровень значимости 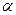 возьмем 0.05.
возьмем 0.05.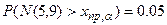 ,
,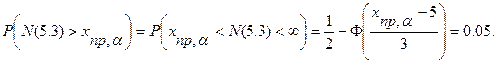
 . По таблицам значений функции
. По таблицам значений функции  находим, что
находим, что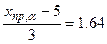 .
. .
. , нужно найти вероятность попадания в область допустимых значений
, нужно найти вероятность попадания в область допустимых значений 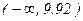 при условии, что гипотеза
при условии, что гипотеза 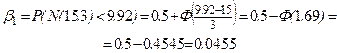
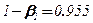 .
. вычисляется из условия
вычисляется из условия
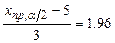 .
.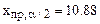 . Левая граница критической области симметрична с точкой
. Левая граница критической области симметрична с точкой 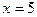 , т.е. левая граница
, т.е. левая граница  . Тогда вероятность ошибки
. Тогда вероятность ошибки  составит
составит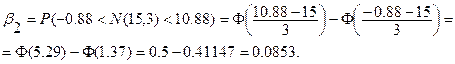
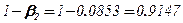 . Значит, односторонняя критическая область больших значений является предпочтительной.
. Значит, односторонняя критическая область больших значений является предпочтительной.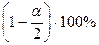 и
и 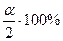 точки, которые делят всю область на 3 части:
точки, которые делят всю область на 3 части: ,
,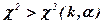 , то гипотеза отвергается, если
, то гипотеза отвергается, если 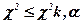 , то гипотеза принимается.
, то гипотеза принимается.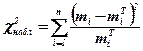 , где
, где 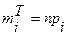 .
.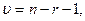 - где r - число параметров предлагаемого теоретического закона, использованных для вычисления теоретических частот.
- где r - число параметров предлагаемого теоретического закона, использованных для вычисления теоретических частот. .
.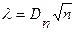 и находится вероятность
и находится вероятность 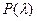 . Функция
. Функция 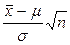 при
при 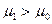 - правосторонняя критическая область
при
- правосторонняя критическая область
при 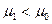 - левосторонняя критическая область
при
- левосторонняя критическая область
при  -двусторонняя критическая область
(нормированный закон распределения)
-двусторонняя критическая область
(нормированный закон распределения)
 Ф(tкр)=1-2α
Ф(tкр)=1-2α
 Ф(tкр)=1-α
Ф(tкр)=1-α
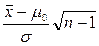 при
при 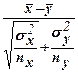 (распределение Стьюдента)
(распределение Стьюдента)
 (распр.Стьюдента)
(распр.Стьюдента)
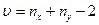 (степень свободы)
(степень свободы)
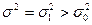

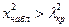 , то нулевая гипотеза H0:
, то нулевая гипотеза H0: 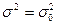 отвергается
отвергается
 , где
, где  исправленные дисперсии
(распределение Фишера-Снедекора(F - распределение))
исправленные дисперсии
(распределение Фишера-Снедекора(F - распределение))
 определяют по таблице F
определяют по таблице F
 , то гипотеза не противоречит опытным данным;
если
, то гипотеза не противоречит опытным данным;
если 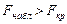 , то гипотезу отвергают.
, то гипотезу отвергают.
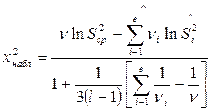 здесь
здесь
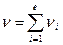
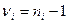 - число степеней
свободы i - той выборки
- число степеней
свободы i - той выборки
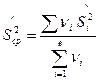 ,
l - кол-во нормальных генеральных совокупностей из которых извлечены выборки. При выполнении нулевой гипотезы и при
,
l - кол-во нормальных генеральных совокупностей из которых извлечены выборки. При выполнении нулевой гипотезы и при  имеет распределение
имеет распределение 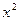 с
с 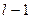 степенью свободы.
степенью свободы.
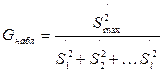 имеет распределение G с
имеет распределение G с 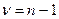 и l степенями свободы, где
и l степенями свободы, где  - наибольшая из исправленных выборочных дисперсий.
- наибольшая из исправленных выборочных дисперсий.
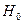 и при
и при  с (
с (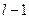 ) степенью свободы.
Применяется, когда объемы выборок извлеченных из генеральных совокупностей равны.
) степенью свободы.
Применяется, когда объемы выборок извлеченных из генеральных совокупностей равны.
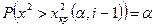 Критерий Кочрана
Если
Критерий Кочрана
Если 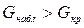 ,
то гипотезу отвергают,
если
,
то гипотезу отвергают,
если  ,
то гипотеза не противоречит опытным значениям.
,
то гипотеза не противоречит опытным значениям.
 . Предполагая, что время изготовления подчиняется нормальному распределению с дисперсией
. Предполагая, что время изготовления подчиняется нормальному распределению с дисперсией 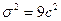 на уровне значимости
на уровне значимости 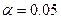 , решить
, решить с. Так как
с. Так как 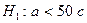 , т.е. имеем случай 2 при
, т.е. имеем случай 2 при 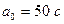 . По изложенной схеме получаем
. По изложенной схеме получаем 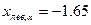 . Подставив исходные данные
. Подставив исходные данные 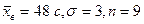 , получаем
, получаем 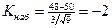 . Так как число –2 попадает в критическую область
. Так как число –2 попадает в критическую область 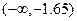 , то гипотеза
, то гипотеза 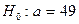 с, альтернативная
с, альтернативная 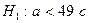 . Снова имеет место случай 2 при
. Снова имеет место случай 2 при 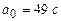 . Так как
. Так как  не попадает в критическую область, то гипотеза
не попадает в критическую область, то гипотеза 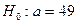 с не отвергается и в качестве норматива времени изготавления детали берем 49 с.
с не отвергается и в качестве норматива времени изготавления детали берем 49 с.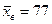 мин, а
мин, а 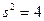 мин2. В предложении о нормальности распределения следует решить: можно ли на уровне значимости
мин2. В предложении о нормальности распределения следует решить: можно ли на уровне значимости 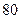 мин нормативом (математическим ожиданием) трудоемкости.
мин нормативом (математическим ожиданием) трудоемкости. мин, в качестве альтернативной
мин, в качестве альтернативной 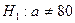 мин, при этом
мин, при этом  . Используя таблицу приложения 5 при
. Используя таблицу приложения 5 при 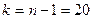 , находим
, находим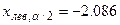 ;
;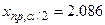 .
.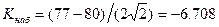 . Так как число
. Так как число 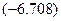 попадает в критическую область (конкретно в интервал
попадает в критическую область (конкретно в интервал  , то гипотеза
, то гипотеза 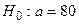 мин отвергается.
мин отвергается.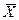 =254°C. Предполагается, что ошибка измерения есть нормальная случайная величина с s = 6°C. На уровне значимости a=0.05 проверить гипотезу H0: m=250°C против гипотезы H1: m=260°C. В ответе записать разность между абсолютными величинами табличного и фактического значений выборочной характеристики.
=254°C. Предполагается, что ошибка измерения есть нормальная случайная величина с s = 6°C. На уровне значимости a=0.05 проверить гипотезу H0: m=250°C против гипотезы H1: m=260°C. В ответе записать разность между абсолютными величинами табличного и фактического значений выборочной характеристики.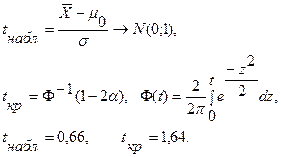
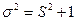 мм2 при конкурирующей гипотезе -
мм2 при конкурирующей гипотезе - 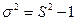 . В ответе записать разность между абсолютными величинами табличного и фактического значений выборочной характеристики.
. В ответе записать разность между абсолютными величинами табличного и фактического значений выборочной характеристики. построим левостороннюю критическую область.
построим левостороннюю критическую область.
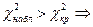 на данном уровне значимости нулевая гипотеза не отвергается (
на данном уровне значимости нулевая гипотеза не отвергается (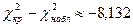 ).
).


