Методы регрессионного и корреляционного анализа 1 страницаОсновной целью изучения причинно-следственной зависимости является выявление связей, закономерностей и тенденций развития. Причинно-следственная зависимость выражает соотношение между функцией (следствием) и аргументом (причиной). Различают две основные формы причинных зависимостей - статистическую и функциональную. При функциональной зависимости каждому возможному значению аргумента поставлено в однозначное соответствие определенное значение функции, т.е. Y = f(X). Но такого рода однозначные (функциональные) связи между переменными величинами встречаются не всегда. Известно, например, что между ростом (длиной тела) и массой человека существует положительная связь - более высокие индивиды имеют обычно и большую массу, чем индивиды низкого роста. То же наблюдается и в отношении качественных признаков - блондины, как правило, имеют голубые, а брюнеты — карие глаза. Однако из этого правила имеются исключения, когда сравнительно низкорослые индивиды оказываются тяжелее высокорослых, и среди населения встречаются кареглазые блондины и голубоглазые брюнеты. Причина таких “исключений” в том, что каждый признак, выражаясь математическим языком, является функцией многих переменных. На его величину оказывает влияние и генетические и средовые факторы, в том числе и случайные, что вызывает варьирование признаков, т.е. в реальности на производимые наблюдения (признаки) воздействуют многочисленные факторы. В этих случаях зависимость между признаками приобретает не функциональный, а статистический характер. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Такого рода зависимость между переменными величинами называется корреляционной или корреляцией (термин “корреляция” происходит от лат. correlatio — соотношение, связь). Статистические связи между переменными можно изучать методами корреляционного и регрессивного анализа. Корреляционный анализ, как и другие статистические методы, основан на использовании вероятностных моделей, описывающих поведение исследуемых признаков в некоторой генеральной совокупности, из которой получены экспериментальные значения xi и yi. Регрессионный анализ заключается в определении аналитического выражения связи, в котором изменение результативного признака обуславливается влиянием одного или нескольких факторных признаков, а множество всех прочих факторов принимается за постоянные (или усредненные) величины. Основная задача корреляционного анализа - выявление связи между случайными переменными путем точечной и интервальных оценок. Метод корреляции применяется для того, чтобы при сложном взаимодействии посторонних влияний выяснить какой должна была быть зависимость между величинами, если бы посторонние факторы не изменялись, и своим изменением не искажали основную зависимость. Теория корреляции решает три основные задачи: § определение корреляционных уравнений связи между двумя и более случайными величинами, § определение тесноты связи и вероятности получаемых характеристик, § обоснование методики проведения исследований по выявлению корреляционных связей. Показателями тесноты между двумя случайными наблюдениями х и y являются коэффициент корреляции
Для нахождения значения знаменателя в формуле коэффициента корреляции среднее квадратическое отклонение величин факторного признака вычисляется по формуле
а результативного — соответственно по формуле:
Коэффициент корреляции не изменяется при изменении начала отсчета и масштаба измерения величин х и y. Он удовлетворяет неравенству Таблица 6.1. Количественные критерии оценки тесноты связи (шкала Чеддока)
Коэффициенты корреляции, как правило, рассчитываются для выборочных данных и поэтому являются случайными величинами. После вычисления r возникает необходимость проверки гипотезы о значимости полученной оценки, то есть распространения полученных частных результатов на генеральную совокупность. При этом допускается некоторая ошибка, которую можно оценить с помощью определенных критериев или понятия средней квадратической ошибки. Средняя квадратическая ошибка для линейного коэффициента корреляции достаточно большой выборки вычисляется по формуле Для оценки значимости r также применяется t-критерий Стьюдента. При этом определяется фактическое значение критерия tr
Исчисленное tr сравнивается с критерием tк, которое берется из таблицы значений t-Стьюдента с учетом заданного уровня значимости α и числа степеней свободы k. Если tr>tк, то величина коэффициента корреляции признается существенной. Коэффициенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определить «полезность» факторного признака при построении уравнения регрессии. Величина коэффициента корреляции служит также оценкой соответствия уравнения регрессии выявленным причинно-следственным связям. К уравнениям регрессионного анализа относятся прямая, гипербола, парабола, экспонента, логарифмическая функция и др. Применение метода наименьших квадратов позволяет получить достаточно точные теоретические значения линии однофакторной регрессии и, соответственно, ее графическое изображение. Подобранной считается та модель расчетов теоретической линии, для которой квадрат отклонений эмпирических данных у от теоретической линии регрессии
Множественные уравнения регрессии позволяют вычислить теоретические значения результативного признака в зависимости от всех включенных в множественное уравнение факторов (без графического его изображения одной теоретической линией). Различный подход к истолкованию результатов регрессионного анализа исходит из разного понимания смысла параметров уравнений регрессии, полученных методом наименьших квадратов. Например, в уравнении однофакторной линейной регрессии При исследовании корреляции между количественными признаками, значения которых можно точно измерить в единицах метрических шкал (рубли, секунды, килограммы и т.д.), очень часто принимается модель двумерной нормально распределенной генеральной совокупности. Такая модель графически отображает зависимость между переменными величинами xi и yi в системе прямоугольных координат. Эту графическую зависимость называют также диаграммой рассеивания или корреляционным полем. Пример. В результате комбинационной группировки 100 рабочих по общему стажу работы и месячной заработной плате получена следующая корреляционная таблица
Для характеристики связи между рассматриваемыми показателями необходимо провести корреляционно-регрессионный анализ двумерной модели. Решение. Обозначим общий производственный стаж рабочих через х, а их месячную заработную плату — через у. Для графического изображения зависимости откладываем в прямоугольной системе координат по оси абсцисс значения группировочного признака-фактора (производственный стаж), а по оси ординат — средние значения зависимого признака (заработную плату).
Рис. 6.1. Корреляционное поле На основе анализа корреляционного поля можно предположить, что между заработной платой и стажем рабочих существует прямая регрессия, уравнение которой будет:
Проведем сначала корреляционный анализ. Основная задача корреляционного анализа (являющаяся основной и в регрессионном анализе) состоит в оценке уравнения регрессии. Для нахождения значений величин a0 и a1, входящих в систему нормальных уравнений, составим расчетные таблицы, введя в них одновременно и величины, необходимые для расчета коэффициента корреляции (в качестве вариант возьмем середины интервалов):
Коэффициент корреляции вычисляется по формуле
Из таблицы определяется величина ∑ тху, равная 187100. Подставим найденные величины в формулу коэффициента корреляции и получим
Полученное значение коэффициента корреляции указывает на наличие достаточно тесной линейной связи между общим производственным стажем и заработной платой рабочих. Если имеются равные интервалы отдельно по факторному и по результативному признакам, как, например, в данной задаче, нахождение коэффициента корреляции целесообразно производить с помощью следующей формулы
где Средняя ошибка коэффициента корреляции определяется по формуле
Отношение коэффициента корреляции к его погрешности равно 13 (0,69:0,052<0,52·3), следовательно, можно считать, что полученный коэффициент корреляции достаточно точно выражает степень связи рассматриваемых показателей. Коэффициент корреляции, уменьшенный на трехкратную величину погрешности, дает гарантийный минимум, а увеличенный на трехкратную величину погрешности — соответственно гарантийный максимум. Так, в данной задаче гарантийный минимум составляет 0,534=0,69—3·0,052, а гарантийный максимум равен 0,846=0,69+З·0.052. Это означает, что для рассматриваемого примера можно ожидать, что не меньше 28,5% (0,534x0,534x100) вариации месячной заработной платы рабочих вызвано вариацией величины общего производственного стажа. Проверим гипотезу Н0 о равенстве нулю генерального коэффициента корреляции против альтернативы Н1 о неравенстве нулю коэффициента корреляции. Для проверки гипотезы Н0 против альтернативы Н1 используем t-критерий Стьюдента с (n-2) степенями свободы Также проверить значимость коэффициента корреляции на уровне α=0,05 можно при помощи критерия Фишера. По таблицам распределения статистики r«Таблица Фишера-Иейтса» получаем: гкр= rтабл(0,05;98)< rтабл(0,05;90)=0,205. Критическая область имеет вид Вычислим коэффициенты уравнения регрессии, для этого подставим найденные значения в систему уравнений и получим:
В результате совместного решения уравнений находим: a0=143,1 и a1=2,89. Искомое уравнение прямой регрессии примет вид:
Это уравнение показывает, что между общим производственным стажем и заработной платой рабочих имеется прямая связь - с увеличением стажа на один год размер месячной заработной платы возрастает в среднем на 2р.89к. (а1). Корреляция и регрессия тесно связаны между собой - первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму. И корреляция, и регрессия служат для установления соотношений между явлениями и для определения наличия или отсутствия связи между ними. Контрольные задания Вариант 1 1. На 1 этаже 9-ти этажного дома в лифт входят 4 человека. Каждый может выйти на одном из 8-ми этажей. Сколькими способами это можно сделать? 2. Эксперимент состоит в том, что одновременно бросают игральную кость и монету. Выпишите все исходы этого эксперимента. 3. Бросаются одновременно две игральные кости. Какова вероятность того, что на второй кости число выпавших очков будет больше, чем на первой? 4. Один преподаватель принимает зачет с положительным исходом с вероятностью 0.8, а другой с вероятностью 0.4. Студент знает, что его шансы попасть ко второму преподавателю 0.7. Найти вероятность того, что студент сдаст зачет. 5. В ящике 3 белых и 5 черных шариков. Из ящика последовательно извлекают 4 раза по одному шарику и запоминают его цвет (каждый раз шарик возвращают обратно). Найти распределение, среднее и дисперсию числа белых шариков. 6. Известна интегральная функция распределения:
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. С целью выявления возможностей оплаты дорожных расходов на работу администрация опросила 50 сотрудников о транспортных затратах. Результаты оказались следующими (руб.): Составить вариационный ряд. Определить статистические характеристики ряда. Построить полигон, гистограмму, кумуляту, огиву. Дать объяснение полученным характеристикам. 2. При обслуживании 200 автомашин в авторемонтной мастерской стоимость разных услуг в среднем составляет 800 рублей. Каких размеров может быть стоимость услуг с вероятностью 0,88% при среднеквадратическом отклонении 500 рублей (считать распределение нормальным). 3. Проверить гипотезу о нормальном распределении, используя различные критерии ряда, представленного в задаче 1. 4. Машина по данным 15 поездок на дорогу из города в пригород едет в среднем 80 мин. Предположив, что время поездок нормальная случайная величина проверить гипотезу 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 2 1. Сколько существует наборов из 6 букв, начинающихся с буквы "а", если буквы не повторяются (используется 30 букв). 2. Из таблицы чисел наугад взято число, событие A - число делится на 3, событие C - число оканчивается нулем. Что означает событие A+ C? Запишите событие, состоящее в том, что число делится на 3 и не делится на 10. 3. На карточках написаны буквы слова "математика". Случайным образом выбирают 4 буквы и составляют из них слово. Найти вероятность того, что в получившемся слове ровно 2 буквы совпадают. 4. Каждое утро экстрасенс, выходя из дому, бросает монету. Если выпадет "герб", то он берет с собой зонтик, иначе выходит без него. При этом, если он выходит из дома с зонтом, то дождь идет с вероятностью 0.3, а если без зонта - то с вероятностью 0.8. Найти вероятность того, что он попадет под дождь. 5. Три спортсмена участвуют в различных видах соревнований. Вероятность выиграть медаль для первого спортсмена - 0.5, для второго - 0.3, для третьего - 0.8. Найти распределение и среднее значение числа завоеванных медалей. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. Измерения подекадной температуры воздуха в некотором районе за 2 года составили следующий ряд (в градусах): Составить вариационный ряд. Определить статистические характеристики ряда. Построить полигон, гистограмму, кумуляту, огиву. Дать объяснение полученным характеристикам. 2. Фирма, торгующая косметикой, изучает спрос у населения. С этой целью проведенный опрос у 500 человек показал, что 35 человек предпочитает покупать производство фирмы "Ромашка". Оценить истинное их количество при 95%-ой доверительности. 3. Проверить гипотезу о нормальном распределении ряда из задачи 1. 4. Лекарство, изготовленное на заводе, испытывалось на пациентах для выяснения побочных эффектов. В эксперименте принимали участие 1000 мужчин и 3000 женщин. Побочные эффекты обнаружились у 70 мужчин и 120 женщин. При уровне значимости α = 0,05 можно ли утверждать при окончании эксперимента, что побочные эффекты у женщин проявляются больше, чем у мужчин. 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
|
,
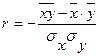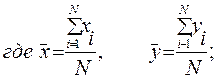
и 
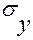- соответствующие средние квадратические отклонения, N - количество независимых наблюдений.
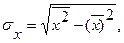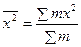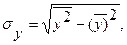где 
,
где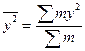 
.
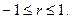. Знак «+» указывает насвязь прямую (увеличение или уменьшение одного признака сопровождается аналогичным изменением другого признака), знак «–» – на связь обратную (увеличение или уменьшение одного признака сопровождается противоположным по направлению изменением другого признака).Если r = ±1, то между величинами существует тесная линейная связь, если r=0, нет линейной корреляционной зависимости (но может быть нелинейная).
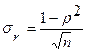, где ρ — коэффициент корреляции генеральной совокупности; n — объем выборки. Коэффициент корреляции достоверен если он больше или равен величине трёх своих ошибок.
.
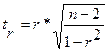минимальный, т.е. 
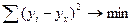. Для определения параметров уравнения на основе требований метода наименьших квадратов необходимо решить систему нормальных уравнений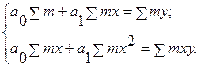
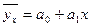параметр a1 означает среднее изменение величины результативного признака у в зависимости от изменения значений факторного признака х, если все остальные факторы, влияющие на результативный признак у и не связанные с факторным, рассматриваются как неизменные. Этот параметр показывает, насколько в среднем величина одного признака Y изменяется при изменении на единицу меры другого корреляционно связанного с Y признака X. Параметр а0 (свободный член) отражает усредненное влияние всех неучтенных факторов. Если первое требование трудно учесть, то второе - истолковать, особенно в тех случаях, когда он имеет отрицательное значение.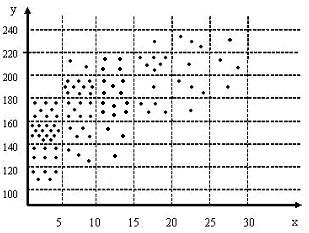
,
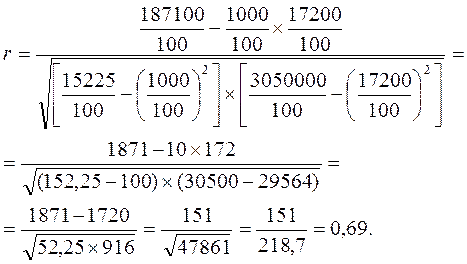
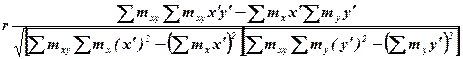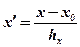и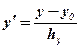 
условные варианты признаков при равных интервалах; тх, ту, и тху — частоты групп и подгрупп по х и у. Так, для рассматриваемой задачи х0=12,5, hх=5, y0=170 и hv = 20. Все дальнейшие вычисления аналогичны рассмотренным ранее.
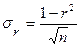, где r — коэффициент корреляции; n — объем совокупности. Подставим в эту формулу полученные данные
.
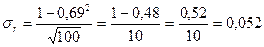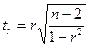. Вычисленное tr сравним с критерием tк, которое возьмем из таблицы значений t-Стьюдента с учетом заданного уровня значения α=0,05 и числа степеней свободы k =(n-2). В нашем примере tr= 
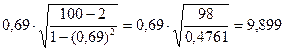, а tк= 1,98. Таким образом, принимается гипотеза Н1 с вероятностью ошибки α=0,05. Полученная оценка коэффициента корреляции является значимой.
. Так, rрасч=0,69 попадает в критическую область (|0,69|>0,205>гкр). Гипотеза Н0:р=0 отвергается с вероятностью ошибки 0,05. Следовательно, коэффициент корреляции р значимо отличается от нуля. Можно считать доказанной связь между случайными величинами х и у.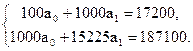
.
.
.
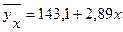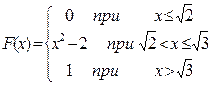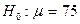мин против конкурирующей гипотезы 
.
.
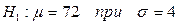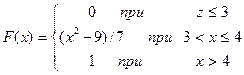