Методы регрессионного и корреляционного анализа 3 страница
5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 10
1. На участие в команде претендует 10 мальчиков и 5 девочек. Сколькими способами можно сформировать команду, состоящую из трех мальчиков и двух девочек?
2. Событие А - выпала карта красной масти, событие В - выпала «дама». Запишите событие, состоящее в том, что а) выпала «дама черной масти»; б) выпала карта черной масти, но это не «дама».
3. В первом ящике - 1 белый, 3 красных и 2 синих шара; во втором - 3 белых, 6 красных, 2 синих. Из каждого ящика вынули по шару. Какова вероятность, что среди вынутых нет синих шаров?
4. В ящике 15 теннисных мячей, среди которых 9 новых. Для первой игры наугад выбирают 2 мяча, которые после игры возвращают обратно. Для второй игры снова берут 2 мяча. Найти вероятность того, что они оба новые (после 1-ой игры новый мяч становится старым).
5. Рабочий обслуживает 2 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего равна для первого станка - 0.9, второго - 0.8. Найти мат.ожидание и дисперсию числа станков, которые не потребуют внимания рабочего в течение часа.
6. Известна интегральная функция распределения
 . .
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций.
________________________________________________________________
1. Число туристов обратившихся в турбюро и желающих посетить какую-то страну регистрировалось в течение месяца. Результаты оказались следующими:
Составить вариационный ряд. Определить статистические характеристики. Построить полигон, гистограмму, кумуляту, огиву. Дать пояснение полученным результатам.
2. При поступлении в институт, где для оценивания знаний принята новая система баллов, протестированы 30 студентов. Получены следующие результаты в баллах
По этим данным найти 95%-ый доверительный интервал для оценки среднего балла тестируемых.
3. В условиях задачи № 1 проверить гипотезу о нормальном распределении.
4. Физическая подготовка 9 спортсменов была проверена при поступлении в спортивную школу, а затем - после недели тренировок. Итоги проверки в баллах оказались следующими (в первой строке указано число баллов, полученных каждым спортсменом при поступлении в школу; во второй строке — после обучения)
Требуется при уровне значимости 0,05 установить, значимо или незначимо улучшилась физическая подготовка спортсменов, в предположении, что число баллов распределено нормально.
5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Рекомендуемая литература
1. Бочаров П.П., Печинкин А.В. Теория вероятностей. Математическая статистика. – М: «Гардарика». 1998.
2. Виленкин Н.Я. Индукция. Комбинаторика. – М., Просвещение. 1976.
3. Воскобойников Ю.Е., Тимошенко Е.И. Математическая статистика. – Новосибирск. 2000.
4. Гнеденко Б.В., Хинчин А.Я. Элементарное введение в теорию вероятностей. – М: Наука. 1982.
5. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учебное пособие – М: Высшая школа. 2006.
6. Гмурман В.Е. Теория вероятностей и математическая статистика: Учебное пособие – М: Высшая школа. 2003.
7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях задачах. Ч.I,II. – М: Оникс 21 век. 2005.
8. Калинина В.Н., Панкин В.Ф. Математическая статистика. – М: Высш. школа. 1994.
9. Карасев А.И. Теория вероятностей и математическая статистика. – М, Статистика. 1970.
10. Колмогоров, А.Н. Основные понятия теории вероятностей. М.: Наука, 1974.
11. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник. – М: Банки и биржи, ЮНИТИ. 2006.
12. Никитина В.Ш. Математическая статистика для экономистов. – М: «ИНФРА-М». 2001.
13. Лихолетов И.И., Мацкевич И.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. – Минск: Высшая школа 1976.
14. Сборник задач по общей теории статистики. – М., Статистика. 1973.
15. Севастьянов Б.А., Чистяков В.П., Зубков А.М. Сборник задач по теории вероятностей. – М:, 1980
16. Статистика. Учебник под ред. И.И. Елисеевой. – СПб: Высшее образование. 2006.
17. Ширяев, А.Н. Вероятность. М: Наука. 1989.
Приложение 1
Таблица функции 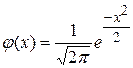 (кривая вероятностей) (кривая вероятностей)
| x
|
|
|
|
|
|
|
|
|
|
| | | 0,0
| 0,3989
| 0,3989
| 0,3989
| 0,3988
| 0,3986
| 0,3984
| 0,3982
| 0,3980
| 0,3977
| 0,3973
| | | 0,1
| 0,3970
| 0,3965
| 0,3961
| 0,3956
| 0,3951
| 0,3945
| 0,3939
| 0,3932
| 0,3925
| 0,3918
| | | 0,2
| 0,3910
| 0,3902
| 0,3894
| 0,3885
| 0,3876
| 0,3867
| 0,3857
| 0,3847
| 0,3836
| 0,3825
| | | 0,3
| 0,3814
| 0,3802
| 0,3790
| 0,3778
| 0,3765
| 0,3752
| 0,3739
| 0,3725
| 0,3712
| 0,3697
| | | 0,4
| 0,3683
| 0,3668
| 0,3653
| 0,3637
| 0,3621
| 0,3605
| 0,3589
| 0,3572
| 0,3555
| 0,3538
| | | 0,5
| 0,3521
| 0,3503
| 0,3485
| 0,3467
| 0,3448
| 0,3429
| 0,3410
| 0,3391
| 0,3372
| 0,3352
| | | 0,6
| 0,3332
| 0,3312
| 0,3292
| 0,3271
| 0,3251
| 0,3230
| 0,3209
| 0,3187
| 0,3166
| 0,3144
| | | 0,7
| 0,3123
| 0,3101
| 0,3079
| 0,3056
| 0,3034
| 0,3011
| 0,2989
| 0,2966
| 0,2943
| 0,2920
| | | 0,8
| 0,2897
| 0,2874
| 0,2850
| 0,2827
| 0,2803
| 0,2780
| 0,2756
| 0,2732
| 0,2709
| 0,2685
| | | 0,9
| 0,2661
| 0,2637
| 0,2613
| 0,2589
| 0,2565
| 0,2541
| 0,2516
| 0,2492
| 0,2468
| 0,2444
| | | 1,0
| 0,2420
| 0,2396
| 0,2371
| 0,2347
| 0,2323
| 0,2299
| 0,2275
| 0,2251
| 0,2227
| 0,2203
| | | 1,1
| 0,2179
| 0,2155
| 0,2131
| 0,2107
| 0,2083
| 0,2059
| 0,2036
| 0,2012
| 0,1989
| 0,1965
| | | 1,2
| 0,1942
| 0,1919
| 0,1895
| 0,1872
| 0,1849
| 0,1826
| 0,1804
| 0,1781
| 0,1758
| 0,1736
| | | 1,3
| 0,1714
| 0,1691
| 0,1669
| 0,1647
| 0,1626
| 0,1604
| 0,1582
| 0,1561
| 0,1539
| 0,1518
| | 1,4
| 0,1497
| 0,1476
| 0,1456
| 0,1435
| 0,1415
| 0,1394
| 0,1374
| 0,1354
| 0,1334
| 0,1315
| | 1,5
| 0,1295
| 0,1276
| 0,1257
| 0,1238
| 0,1219
| 0,1200
| 0,1182
| 0,1163
| 0,1145
| 0,1127
| | 1,6
| 0,1109
| 0,1092
| 0,1074
| 0,1057
| 0,1040
| 0,1023
| 0,1006
| 0,0989
| 0,0973
| 0,0957
| | 1,7
| 0,0940
| 0,0925
| 0,0909
| 0,0893
| 0,0878
| 0,0863
| 0,0848
| 0,0833
| 0,0818
| 0,0804
| | 1,8
| 0,0790
| 0,0775
| 0,0761
| 0,0748
| 0,0734
| 0,0721
| 0,0707
| 0,0694
| 0,0681
| 0,0669
| | 1,9
| 0,0656
| 0,0644
| 0,0632
| 0,0620
| 0,0608
| 0,0596
| 0,0584
| 0,0573
| 0,0562
| 0,0551
| | 2,0
| 0,0540
| 0,0529
| 0,0519
| 0,0508
| 0,0498
| 0,0488
| 0,0478
| 0,0468
| 0,0459
| 0,0449
| | 2,1
| 0,0440
| 0,0431
| 0,0422
| 0,0413
| 0,0404
| 0,0396
| 0,0387
| 0,0379
| 0,0371
| 0,0363
| | 2,2
| 0,0355
| 0,0347
| 0,0339
| 0,0332
| 0,0325
| 0,0317
| 0,0310
| 0,0303
| 0,0297
| 0,0290
| | 2,3
| 0,0283
| 0,0277
| 0,0270
| 0,0264
| 0,0258
| 0,0252
| 0,0246
| 0,0241
| 0,0235
| 0,0229
| | 2,4
| 0,0224
| 0,0219
| 0,0213
| 0,0208
| 0,0203
| 0,0198
| 0,0194
| 0,0189
| 0,0184
| 0,0180
| | 2,5
| 0,0175
| 0,0171
| 0,0167
| 0,0163
| 0,0158
| 0,0154
| 0,0151
| 0,0147
| 0,0143
| 0,0139
| | 2,6
| 0,0136
| 0,0132
| 0,0129
| 0,0126
| 0,0122
| 0,0119
| 0,0116
| 0,0113
| 0,0110
| 0,0107
| | 2,7
| 0,0104
| 0,0101
| 0,0099
| 0,0096
| 0,0093
| 0,0091
| 0,0088
| 0,0086
| 0,0084
| 0,0081
| | 2,8
| 0,0079
| 0,0077
| 0,0075
| 0,0073
| 0,0071
| 0,0069
| 0,0067
| 0,0065
| 0,0063
| 0,0061
| | 2,9
| 0,0060
| 0,0058
| 0,0056
| 0,0055
| 0,0053
| 0,0051
| 0,0050
| 0,0048
| 0,0047
| 0,0046
| | 3,0
| 0,0044
| 0,0043
| 0,0042
| 0,0040
| 0,0039
| 0,0038
| 0,0037
| 0,0036
| 0,0035
| 0,0034
| | 3,1
| 0,0033
| 0,0032
| 0,0031
| 0,0030
| 0,0029
| 0,0028
| 0,0027
| 0,0026
| 0,0025
| 0,0025
| | 3,2
| 0,0024
| 0,0023
| 0,0022
| 0,0022
| 0,0021
| 0,0020
| 0,0020
| 0,0019
| 0,0018
| 0,0018
| | 3,3
| 0,0017
| 0,0017
| 0,0016
| 0,0016
| 0,0015
| 0,0015
| 0,0014
| 0,0014
| 0,0013
| 0,0013
| | 3,4
| 0,0012
| 0,0012
| 0,0012
| 0,0011
| 0,0011
| 0,0010
| 0,0010
| 0,0010
| 0,0009
| 0,0009
| | 3,5
| 0,0009
| 0,0008
| 0,0008
| 0,0008
| 0,0008
| 0,0007
| 0,0007
| 0,0007
| 0,0007
| 0,0006
| | 3,6
| 0,0006
| 0,0006
| 0,0006
| 0,0005
| 0,0005
| 0,0005
| 0,0005
| 0,0005
| 0,0005
| 0,0004
| | 3,7
| 0,0004
| 0,0004
| 0,0004
| 0,0004
| 0,0004
| 0,0004
| 0,0003
| 0,0003
| 0,0003
| 0,0003
| | 3,8
| 0,0003
| 0,0003
| 0,0003
| 0,0003
| 0,0003
| 0,0002
| 0,0002
| 0,0002
| 0,0002
| 0,0002
| | 3,9
| 0,0002
| 0,0002
| 0,0002
| 0,0002
| 0,0002
| 0,0002
| 0,0002
| 0,0002
| 0,0001
| 0,0001
| | 4,0
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| | 4,1
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| | 4,2
| 0,0001
| 0,0001
| 0,0001
| 0,0001
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| | | | | | | | | | | | | | | | | | | | | | | | | | | | Приложение 2
Таблица функции 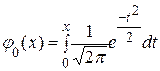 (функция Лапласа) (функция Лапласа)
| x
|
|
|
|
|
|
|
|
|
|
| | | 0,0
| 0,00000
| 0,00399
| 0,00798
| 0,01197
| 0,01595
| 0,01994
| 0,02392
| 0,02790
| 0,03188
| 0,03586
| | | 0,1
| 0,03983
| 0,04380
| 0,04776
| 0,05172
| 0,05567
| 0,05962
| 0,06356
| 0,06749
| 0,07142
| 0,07535
| | | 0,2
| 0,07926
| 0,08317
| 0,08706
| 0,09095
| 0,09483
| 0,09871
| 0,10257
| 0,10642
| 0,11026
| 0,11409
| | | 0,3
| 0,11791
| 0,12172
| 0,12552
| 0,12930
| 0,13307
| 0,13683
| 0,14058
| 0,14431
| 0,14803
| 0,15173
| | | 0,4
| 0,15542
| 0,15910
| 0,16276
| 0,16640
| 0,17003
| 0,17364
| 0,17724
| 0,18082
| 0,18439
| 0,18793
| | | 0,5
| 0,19146
| 0,19497
| 0,19847
| 0,20194
| 0,20540
| 0,20884
| 0,21226
| 0,21566
| 0,21904
| 0,22240
| | | 0,6
| 0,22575
| 0,22907
| 0,23237
| 0,23565
| 0,23891
| 0,24215
| 0,24537
| 0,24857
| 0,25175
| 0,25490
| | | 0,7
| 0,25804
| 0,26115
| 0,26424
| 0,26730
| 0,27035
| 0,27337
| 0,27637
| 0,27935
| 0,28230
| 0,28524
| | | 0,8
| 0,28814
| 0,29103
| 0,29389
| 0,29673
| 0,29955
| 0,30234
| 0,30511
| 0,30785
| 0,31057
| 0,31327
| | | 0,9
| 0,31594
| 0,31859
| 0,32121
| 0,32381
| 0,32639
| 0,32894
| 0,33147
| 0,33398
| 0,33646
| 0,33891
| | | 1,0
| 0,34134
| 0,34375
| 0,34614
| 0,34849
| 0,35083
| 0,35314
| 0,35543
| 0,35769
| 0,35993
| 0,36214
| | | 1,0
| 0,36433
| 0,36650
| 0,36864
| 0,37076
| 0,37286
| 0,37493
| 0,37698
| 0,37900
| 0,38100
| 0,38298
| | | 1,2
| 0,38493
| 0,38686
| 0,38877
| 0,39065
| 0,39251
| 0,39435
| 0,39617
| 0,39796
| 0,39973
| 0,40147
| | | 1,3
| 0,40320
| 0,40490
| 0,40658
| 0,40824
| 0,40988
| 0,41149
| 0,41308
| 0,41466
| 0,41621
| 0,41774
| | | 1,4
| 0,41924
| 0,42073
| 0,42220
| 0,42364
| 0,42507
| 0,42647
| 0,42785
| 0,42922
| 0,43056
| 0,43189
| | | 1,5
| 0,43319
| 0,43448
| 0,43574
| 0,43699
| 0,43822
| 0,43943
| 0,44062
| 0,44179
| 0,44295
| 0,44408
| | | 1,6
| 0,44520
| 0,44630
| 0,44738
| 0,44845
| 0,44950
| 0,45053
| 0,45154
| 0,45254
| 0,45352
| 0,45449
| | | 1,7
| 0,45543
| 0,45637
| 0,45728
| 0,45818
| 0,45907
| 0,45994
| 0,46080
| 0,46164
| 0,46246
| 0,46327
| | | 1,8
| 0,46407
| 0,46485
| 0,46562
| 0,46638
| 0,46712
| 0,46784
| 0,46856
| 0,46926
| 0,46995
| 0,47062
| | | 1,9
| 0,47128
| 0,47193
| 0,47257
| 0,47320
| 0,47381
| 0,47441
| 0,47500
| 0,47558
| 0,47615
| 0,47670
| | | 2,0
| 0,47725
| 0,47778
| 0,47831
| 0,47882
| 0,47932
| 0,47982
| 0,48030
| 0,48077
| 0,48124
| 0,48169
| | | 2,1
| 0,48214
| 0,48257
| 0,48300
| 0,48341
| 0,48382
| 0,48422
| 0,48461
| 0,48500
| 0,48537
| 0,48574
| | | 2,2
| 0,48610
| 0,48645
| 0,48679
| 0,48713
| 0,48745
| 0,48778
| 0,48809
| 0,48840
| 0,48870
| 0,48899
| | | 2,3
| 0,48928
| 0,48956
| 0,48983
| 0,49010
| 0,49036
| 0,49061
| 0,49086
| 0,49111
| 0,49134
| 0,49158
| | | 2,4
| 0,49180
| 0,49202
| 0,49224
| 0,49245
| 0,49266
| 0,49286
| 0,49305
| 0,49324
| 0,49343
| 0,49361
| | | 2,5
| 0,49379
| 0,49396
| 0,49413
| 0,49430
| 0,49446
| 0,49461
| 0,49477
| 0,49492
| 0,49506
| 0,49520
| | | 2,6
| 0,49534
| 0,49547
| 0,49560
| 0,49573
| 0,49585
| 0,49598
| 0,49609
| 0,49621
| 0,49632
| 0,49643
| | | 2,7
| 0,49653
| 0,49664
| 0,49674
| 0,49683
| 0,49693
| 0,49702
| 0,49711
| 0,49720
| 0,49728
| 0,49736
| | | 2,8
| 0,49744
| 0,49752
| 0,49760
| 0,49767
| 0,49774
| 0,49781
| 0,49788
| 0,49795
| 0,49801
| 0,49807
| | 2,9
| 0,49813
| 0,49819
| 0,49825
| 0,49831
| 0,49836
| 0,49841
| 0,49846
| 0,49851
| 0,49856
| 0,49861
| | 3,0
| 0,49865
| 0,49869
| 0,49874
| 0,49878
| 0,49882
| 0,49886
| 0,49889
| 0,49893
| 0,49896
| 0,49900
| | 3,1
| 0,49903
| 0,49906
| 0,49910
| 0,49913
| 0,49916
| 0,49918
| 0,49921
| 0,49924
| 0,49926
| 0,49929
| | 3,2
| 0,49931
| 0,49934
| 0,49936
| 0,49938
| 0,49940
| 0,49942
| 0,49944
| 0,49946
| 0,49948
| 0,49950
| | 3,3
| 0,49952
| 0,49953
| 0,49955
| 0,49957
| 0,49958
| 0,49960
| 0,49961
| 0,49962
| 0,49964
| 0,49965
| | 3,4
| 0,49966
| 0,49968
| 0,49969
| 0,49970
| 0,49971
| 0,49972
| 0,49973
| 0,49974
| 0,49975
| 0,49976
| | 3,5
| 0,49977
| 0,49978
| 0,49978
| 0,49979
| 0,49980
| 0,49981
| 0,49981
| 0,49982
| 0,49983
| 0,49983
| | 3,6
| 0,49984
| 0,49985
| 0,49985
| 0,49986
| 0,49986
| 0,49987
| 0,49987
| 0,49988
| 0,49988
| 0,49989
| | 3,7
| 0,49989
| 0,49990
| 0,49990
| 0,49990
| 0,49991
| 0,49991
| 0,49992
| 0,49992
| 0,49992
| 0,49992
| | 3,8
| 0,49993
| 0,49993
| 0,49993
| 0,49994
| 0,49994
| 0,49994
| 0,49994
| 0,49995
| 0,49995
| 0,49995
| | 3,9
| 0,49995
| 0,49995
| 0,49996
| 0,49996
| 0,49996
| 0,49996
| 0,49996
| 0,49996
| 0,49997
| 0,49997
| | 4,0
| 0,499968
| | 4,5
| 0,49997
| | 5,0
| 0,4999997
| | | | | | | | | | | | | | | | | | | | | | | | | | | Приложение 3
Таблица значений функции Пуассона: 
| m
| λ
| 0,1
| 0,2
| 0,3
| 0,4
| 0,5
| 0,6
| 0,7
| 0,8
| 0,9
| |
| 0,9048
| 0,8187
| 0,7408
| 0,6703
| 0,6065
| 0,5488
| 0,4966
| 0,4493
| 0,4066
| |
| 0,0905
| 0,1638
| 0,2222
| 0,2681
| 0,3033
| 0,3293
| 0,3476
| 0,3596
| 0,3696
| |
| 0,0045
| 0,0164
| 0,0333
| 0,0536
| 0,0758
| 0,0988
| 0,1217
| 0,1438
| 0,1647
| |
| 0,0002
| 0,0011
| 0,0033
| 0,0072
| 0,0126
| 0,0198
| 0,0284
| 0,0383
| 0,0494
| |
| 0,0000
| 0,0000
| 0,0002
| 0,0007
| 0,0016
| 0,0030
| 0,0050
| 0,0077
| 0,0111
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0001
| 0,0002
| 0,0004
| 0,0007
| 0,0012
| 0,0020
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0001
| 0,0002
| 0,0003
| | m
| λ
| 1,0
| 2,0
| 3,0
| 4,0
| 5,0
| 6,0
| 7,0
| 8,0
| 9,0
| |
| 0,3679
| 0,1353
| 0,0498
| 0,0183
| 0,0067
| 0,0025
| 0,0009
| 0,0003
| 0,0001
| |
| 0,3679
| 0,2707
| 0,1494
| 0,0733
| 0,0337
| 0,0149
| 0,0064
| 0,0027
| 0,0011
| |
| 0,1839
| 0,2707
| 0,2240
| 0,1465
| 0,0842
| 0,0446
| 0,0223
| 0,0107
| 0,0055
| |
| 0,0613
| 0,1804
| 0,2240
| 0,1954
| 0,1404
| 0,0892
| 0,0521
| 0,0286
| 0,0150
| |
| 0,0153
| 0,0902
| 0,1680
| 0,1954
| 0,1755
| 0,1339
| 0,0912
| 0,0572
| 0,0337
| |
| 0,0081
| 0,0361
| 0,1008
| 0,1563
| 0,1755
| 0,1606
| 0,1277
| 0,0916
| 0,0607
| | m
| λ
| 1,0
| 2,0
| 3,0
| 4,0
| 5,0
| 6,0
| 7,0
| 8,0
| 9,0
| |
| 0,0005
| 0,0120
| 0,0504
| 0,1042
| 0,1462
| 0,1606
| 0,1490
| 0,1221
| 0,0911
| |
| 0,0001
| 0,0034
| 0,0216
| 0,0595
| 0,1044
| 0,1377
| 0,1490
| 0,1396
| 0,1318
| |
| 0,0000
| 0,0009
| 0,0081
| 0,0298
| 0,0655
| 0,1033
| 0,1304
| 0,1396
| 0,1318
| |
| 0,0000
| 0,0002
| 0,0027
| 0,0132
| 0,0363
| 0,0688
| 0,1014
| 0,1241
| 0,0318
| |
| 0,0000
| 0,0000
| 0,0008
| 0,0053
| 0,0181
| 0,0413
| 0,0710
| 0,0993
| 0,1180
| |
| 0,0000
| 0,0000
| 0,0002
| 0,0019
| 0,0082
| 0,0225
| 0,0452
| 0,0722
| 0,0970
| |
| 0,0000
| 0,0000
| 0,0001
| 0,0006
| 0,0034
| 0,0113
| 0,0264
| 0,0481
| 0,0728
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0002
| 0,0013
| 0,0052
| 0,0142
| 0,0296
| 0,0504
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0001
| 0,0005
| 0,0022
| 0,0071
| 0,0169
| 0,0324
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0002
| 0,0009
| 0,0033
| 0,0090
| 0,0194
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000.
| 0,0003
| 0,0014
| 0,0045
| 0,0109
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0001
| 0,0006
| 0,0021
| 0,0058
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0002
| 0,0009
| 0,0029
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0001
| 0,0004
| 0,0014
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0002
| 0,0006
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0001
| 0,0003
| |
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0000
| 0,0001
| | | | | | | | | | | | | | | |

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Потенциометрия. Потенциометрическое определение рН растворов Потенциометрия - это электрохимический метод исследования и анализа веществ, основанный на зависимости равновесного электродного потенциала Е от активности (концентрации) определяемого вещества в исследуемом растворе...
Гальванического элемента При контакте двух любых фаз на границе их раздела возникает двойной электрический слой (ДЭС), состоящий из равных по величине, но противоположных по знаку электрических зарядов...
Сущность, виды и функции маркетинга персонала Перснал-маркетинг является новым понятием. В мировой практике маркетинга и управления персоналом он выделился в отдельное направление лишь в начале 90-х гг.XX века...
|
Виды сухожильных швов После выделения культи сухожилия и эвакуации гематомы приступают к восстановлению целостности сухожилия...
КОНСТРУКЦИЯ КОЛЕСНОЙ ПАРЫ ВАГОНА Тип колёсной пары определяется типом оси и диаметром колес. Согласно ГОСТ 4835-2006* устанавливаются типы колесных пар для грузовых вагонов с осями РУ1Ш и РВ2Ш и колесами диаметром по кругу катания 957 мм. Номинальный диаметр колеса – 950 мм...
Философские школы эпохи эллинизма (неоплатонизм, эпикуреизм, стоицизм, скептицизм). Эпоха эллинизма со времени походов Александра Македонского, в результате которых была образована гигантская империя от Индии на востоке до Греции и Македонии на западе...
|
|

 .
.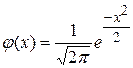 (кривая вероятностей)
(кривая вероятностей)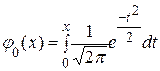 (функция Лапласа)
(функция Лапласа)



