Решение. Условное математическое ожидание случайной величины
p(x1)=0.15+0.30=0.45, p(y1/x1 )= p(x1 ,y1 )/p(x1)=0.15/0.45=1/3, p(y2/x1 )= p(x1 ,y2 )/p(x1)=0.30/0.45=2/3, => Условное математическое ожидание случайной величины при условии, что другая случайная величина приняла заданное значение, определяет число-точку, относительно которой группируются результаты конкретных испытаний над одной случайной величиной при условии, что в этом испытании (над двумерной случайной величиной XY) вторая случайная величина приняла заданное фиксированное значение. Условная дисперсия определяет степень концентрации результатов конкретных испытаний над одной случайной величиной относительно условного математического ожидания. При решении практических задач условное математическое ожидание и условная дисперсия обычно используются, когда при проведении испытания над X и Y, имеется возможность измерять результаты испытания над одной случайной величиной, а измерение другой недоступно. Если условные дисперсии малы, то в качестве неизвестного значения не измеряемой случайной величины можно взять математическое ожидание.
§ 5. Закон больших чисел Закон больших чисел – общий принцип, в силу которого совместное действие случайных факторов приводит при некоторых общих условиях к результату, почти не зависящему от случая. Единичные явления в большей степени подвержены воздействию случайных и несущественных факторов, чем их масса в целом. При большом числе наблюдений случайные отклонения погашаются. Под законом больших чисел понимается ряд математических теорем, в которых устанавливаются факты приближения средних характеристик большого числа опытов к некоторым определенным постоянным. Теорема Чебышева. Если Х 1, Х 2,…, Хп –независимые случайные величины, дисперсии которых равномерно ограничены (D (Xi) ≤ C), то для сколь угодно малого числа ε вероятность неравенства
будет сколь угодно близка к 1, если число случайных величин достаточно велико. Вывод: среднее арифметическое достаточно большого числа случайных величин принимает значения, близкие к сумме их математических ожиданий, то есть утрачивает характер случайной величины. Например, если проводится серия измерений какой-либо физической величины, причем: а) результат каждого измерения не зависит от результатов остальных, то есть все результаты представляют собой попарно независимые случайные величины; б) измерения производятся без систематических ошибок (их математические ожидания равны между собой и равны истинному значению а измеряемой величины); в) обеспечена определенная точность измерений, следовательно, дисперсии рассматриваемых случайных величин равномерно ограничены; то при достаточно большом числе измерений их среднее арифметическое окажется сколь угодно близким к истинному значению измеряемой величины. Теорема Чебышева дает одну из наиболее возможных форм закона больших чисел. Она устанавливает связь между средним арифметическим и ее математическим ожиданием наблюдаемых значений случайной величины. Доказательство этой теоремы основывается на неравенстве Чебышева: P( | X – M (X)| ≤ ε) > 1- D (X)/ε². Пример. Для определения среднего дохода налогоплательщиков города налоговой инспекцией была проведена проверка 250 жителей этого города, отобранных случайным образом. Оценить вероятность того, что средний годовой доход жителей города отклонится от среднего арифметического Решение. Согласно неравенству Чебышева, которым можно пользоваться, поскольку все
Теорема Бернулли. Если в каждом из п независимых опытов вероятность р появления события А постоянна, то при достаточно большом числе испытаний вероятность того, что модуль отклонения относительной частоты появлений А в п опытах от р будет сколь угодно малым, как угодно близка к 1:
Замечание. Из теоремы Бернулли не следует, что Рассмотрим справедливость этого утверждения на историческом примере. При бросании монеты и «герб», и «решка» имеют одинаковые шансы оказаться сверху, таким образом, вероятность выпадения «герба» равна ½ из соображений равновозможности. Французский естествоиспытатель XVIII века Бюффон бросил монету 4040 раз, «герб» выпал при этом 2048 раз. Частота появления «герба» в опыте Бюффона равна 0,507. Английский статистик К.Пирсон бросил монету 12000 раз и при этом наблюдал 6019 выпадений «герба» – частота 0,5016. В другой раз он бросил монету 24000 раз, «герб» выпал 12012 раз – частота 0,5005. Как видим, во всех этих случаях частоты лишь незначительно отличаются от теоретической вероятности 0,5. Теорема Бернулли дает возможность связать математическое определение вероятности (по А.Н.Колмогорову) с определением ряда естествоиспытателей, согласно которому вероятность есть предел частоты в бесконечной последовательности испытаний. Вопрос исследования вида предельного закона распределения суммы случайных величин рассмотрен в группе теорем, которые носят название центральной предельной теоремы (ЦПТ). Эти теоремы утверждают, что закон распределения суммы случайных величин, каждая из которых может иметь различные распределения, приближается к нормальному при достаточно большом числе слагаемых. Этим объясняется важность нормального закона для практических приложений. Рассмотрим одну из наиболее общих форм центральной предельной теоремы: Центральная предельная теорема. Пусть имеется взвешенная сумма независимых случайных непрерывных величин x1, x2, x3, …., xn с произвольными законами распределения:
где
Тогда при достаточно общих условиях распределения суммарной Yn при Центральной предельной теоремой пользуются для приближённого вычисления вероятностей, связанных с суммами большого числа независимых и одинаково распределённых величин. Опыт показывает, что для суммы даже десяти и менее слагаемых закон их распределения можно заменить нормальным. Частным случаем центральной предельной теоремы для дискретных случайных величин является теорема Муавра-Лапласа. Элементы математической статистики § 1. Предмет математической статистики Для решения задач, связанных с анализом информации при наличии фактора случайности, разработана совокупность методов, которая носит название математической статистики. Математическая статистика – это раздел математики, занимающийся разработкой методов сбора, регистрации, систематизации результатов многократных наблюдений с целью познания массовых явлений и процессов. Методы математической статистики позволяют анализировать результаты опытов (наблюдений) и на основе анализа строить оптимальные математико-статистические модели изучаемых явлений и процессов. Исследование математико-статистических моделей позволяет делать обоснованные выводы и прогнозы, решать задачи прогнозирования в различных сферах человеческой деятельности. Математическая статистика возникла в 17 веке и развивалась параллельно с теорией вероятностей. Между основными понятиями в математической статистике и теории вероятностей существует тесная взаимосвязь, которая обосновывает практическую ценность теории вероятностей и подтверждает теоретическую основу математической статистики. Общим для статистических и вероятностных характеристик является техника их вычислений. Главное различие между ними состоит в том, что статистические характеристики относятся к эмпирическим, а вероятностные к теоретическим понятиям. Статистические характеристики - это величины, которые при соблюдении определенных условий стремятся к вероятностным. Вероятностные характеристики можно рассматривать как предельные значения сопоставимых им характеристик математической статистики при возрастании числа наблюдений или опытов. Закономерность, проявляющаяся лишь в большой массе явлений через преодоление свойственной ее единичным элементам случайности, называется статистической закономерностью. Первая теорема, установившая связь между теорией (теория вероятностей) и ее практической стороной (математическая статистика) была доказана в конце 17 века Якобом Бернулли (При соединении большого числа случайных явлений в общих характеристиках всей массы случайность исчезает в тем большей мере, чем больше соединено единичных явлений.). Эта теорема дала начало развитию предельных теорем. Несмотря на колебания отдельных результатов наблюдений при повторных измерениях проявляется определенная закономерность (устойчивость). Она состоит в том, что средний результат при большом числе наблюдений не зависит от отдельных наблюдений. Основные понятия теории вероятностей и математической статистики тождественны, но не равны в смысле их количественного выражения. Их можно сопоставить следующим образом:
Задачи математической статистики можно разбить на три типа: § определение неизвестного закона распределения случайной величины, § определение параметров распределения и их оценка, § проверка правдоподобия гипотез о распределении статистических параметров. Математическая статистика указывает, как наилучшим способом использовать имеющуюся информацию для получения по возможности более точных характеристик массового явления. Методы статистического анализа являются универсальными и могут применяться в самых различных областях человеческой деятельности.
§ 2. Выборочная совокупность и ее характеристики Перед построением и анализом модели, описывающей исследуемое массовое явление или некоторый процесс, необходим сбор опытных данных результатов обследования объектов, отображающих массовое явление. Пусть произведено n независимых испытаний, в результате которых получены некоторые значения X1, X2, X3,………Xn. Совокупность, состоящая из всех возможных в данных условиях наблюдений, обладающих качественной общностью и подлежащих исследованию называется генеральной совокупностью. Генеральная совокупность содержит достаточно большое количество элементов, поэтому обычно производится анализ некоторого ограниченного количества элементов взятых из генеральной совокупности. На основе анализа делаются выводы о генеральной совокупности или, другими словами, обо всей вероятной ситуации. Таким образом, задачи математической статистики практически сводятся к обоснованному суждению об объективных свойствах генеральной совокупности по результатам случайной выборки. Выборочной совокупностью (выборкой) называется множество наблюдений, отобранных из генеральной совокупности. Выборка должна правильно отражать пропорции генеральной совокупности (быть репрезентативной), то есть все объекты генеральной совокупности должны иметь одинаковую вероятность попасть в выборку. Репрезентативность выборки обеспечивается случайностью отбора объектов. При отборе объектов в выборочную совокупность возможны два варианта: § объект возвращается в генеральную совокупность. Выборочная совокупность, полученная таким образом, называется случайной выборкой с возвратом или повторной выборкой, § объект, включенный в выборку, не возвращается назад в генеральную совокупность. Такая выборка называется случайной выборкой без возврата (или бесповторной выборкой). Очевидно, что в повторной выборке возможна ситуация, когда один и тот же объект будет обследован несколько раз. Если объем генеральной совокупности велик, то различие между повторной и бесповторной выборками (которые составляют небольшую часть генеральной совокупности) незначительно. В таких случаях, как правило, используют выборку без возврата. Если генеральная совокупность имеет не очень большой объем, то различие между указанными выборками будет существенным. Отдельные значения генеральной совокупности X1, X2, X3,………Xn называются вариантами признака. Если F(x) – функция распределения генеральной совокупности X, то у каждой случайной величины Xi функция распределения также равна F(x). Понятно, что получить n значений случайной величины X все равно, что получить одно значение n - мерной случайной величины (X1, X2, X3,………Xn). Поэтому каждую выборку x1, x2, x3,………xn объема n мы можем рассматривать как одно значение Числа, показывающие, сколько раз наблюдается определенная варианта, называют частотами (m1, m2……..m n). Расположив варианты в возрастающем или убывающем порядке (ранжирование ряда) и поставив в соответствие с этими вариантами их частоты, получим упорядоченный ряд. Такой ряд называется вариационным рядом. Все возможные значения признака, принимающие изолированные значения, отличающиеся на некоторую конечную величину, называются дискретными. Значения признака, принимаемые в некотором числовом интервале, называют непрерывными. Помимо частоты в статистике используется понятие накопленной частоты, показывающей, сколько наблюдалось элементов со значением признака меньшим или равным Отношение частоты (накопленной частоты) к общему числу наблюдений называется частостью (накопленной частостью) и обозначается
Накопленные частоты выражаются в относительных числах или в процентах. В дискретном вариационном ряду, накопленные частоты и частости являются результатом последовательного суммирования частот и частостей, начиная от первой варианты. Пример. На телефонной станции проводилось исследование качества ее работы. Для исследования измеряли число неправильных соединений в минуту (X). В течение часа были получены следующие 60 значений наблюдаемого признака: Очевидно, что X является дискретной случайной величиной, и полученные данные являются значениями этой случайной величины. Анализ данных, представленных в таблице, затруднителен, поэтому произведем группировку. В результате группировки получено семь значений случайной величины (варианты): 0; 1; 2; 3; 4; 5; 7. При этом значение 0 в этой группе встречается 8 раз, значение 1 – 13 раз, значение 2 – 17 раз, значение 3 – 11 раз, значение 4 – 7 раз, значение 5 – 2 раза, значение 7 – 1 раз. Вычисленные значения частот и частостей запишем в таблицу:
Полученный дискретный ряд представлен в таблице: где во второй строке указаны соответствующие частоты. В отличие от исходных данных этот ряд позволяет делать некоторые выводы о статистических закономерностях. Если число возможных значений дискретной случайной величины достаточно велико или наблюдаемая случайная величина является непрерывной, то строят интервальный вариационный ряд. Под интервальным вариационным рядом понимают упорядоченную совокупность интервалов варьирования значений случайной величины и соответствующие частоты или частости попаданий в каждый интервал значений случайной величины. Как правило, частичные интервалы, на которые разбивается весь интервал варьирования, имеют одинаковую длину и представимы в виде
где L - число интервалов, h – длина интервала. Длину h следует выбирать так, чтобы построенный ряд не был громоздким, но в то же время позволял выявлять характерные изменения случайной величины. Рекомендуется для вычисления h использовать формулу Стерджеса:
где
После нахождения частичных интервалов определяется сколько значений случайной величины попадает в каждый конкретный интервал. При этом в интервал включают значения большие или равные нижней границе и меньшие верхней границы. Одной из основных характеристик выборки является выборочная (эмпирическая) функция распределения:
где Из определения следует, что функция 1. 2. 3. Как известно, аналогичными свойствами обладает и функция распределения F(x). Для приближенного представления теоретической функции распределения F(x) случайной величины X, которую наблюдаем в эксперименте, целесообразно использовать эмпирическую функцию распределения выборки Пример. Используя дискретный вариационный ряд, полученный в предыдущем примере, вычислим значения
Графическое изображение вариационных рядов дает наглядное представление о распределении. По данным таблицы построим график выборочной функции распределения (рис. 2.1).
Рис. 2.1. График выборочной функции распределения (накопленных частот) Характер изменения значений частот (частостей) наглядно представляется в виде графического изображения вариационных рядов. Наиболее простым способом графического изображения вариационных рядов является точечная диаграмма. Кроме точечной диаграммы применяются следующие формы: полигон, гистограмма, кумулята, огива. Полигон - графическое изображение вариационного ряда в виде многоугольника, при этом по горизонтальной оси откладываются значения признака, а по вертикальной – частота встречаемости соответствующего значения признака. Гистограмма - ряд прямоугольников, основания которых равны ширине интервала, а высоты частоте или частости. Гистограмма позволяет «зрительно» определить нормальность эмпирического распределения. Гистограмма позволяет качественно оценить различные характеристики распределения. Например на ней можно увидеть, что распределение бимодально (имеет 2 пика). Это может быть вызвано, например, тем, что выборка неоднородна, возможно, извлечена из двух разных генеральных совокупностей, каждая из которых более или менее нормальна. Кумулята – графическое изображение вариационного ряда с накопленными частотами. Огива – графическое изображение вариационного ряда с накопленными частотами, но в отличие от кумуляты по вертикальной оси откладываются значения признака, а по горизонтальной накопленные частоты (частости). Пример. Распределение предприятий по издержкам обращения (млн.руб.), полученным в отчетном периоде, представлено в ранжированном виде интервалами объема издержек обращения xj и количеством nj предприятий, издержки которых попадают в j интервал.
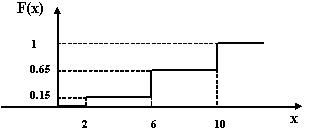
Общее количество предприятий По данным таблицы построим график выборочной функции распределения или график накопленных частот (рис. 2.2) и полигон частот (рис.2.3).
Рис. 2.2. График выборочной функции распределения (накопленных частот)
Рис. 2.3. Полигон частот случайной величины Также для данных примера
построим гистограмму частот (рис. 2.4).
Рис. 2.4. Гистограмма частот случайной величины Рассмотренная выборочная функция распределения и гистограмма позволяют делать выводы о закономерностях исследуемого массового явления, но при анализе данных возникает вопрос об описании их положения, разброса, характере разброса. Для этого используются числовые характеристики выборочной совокупности, из которых сначала рассмотрим выборочное среднее и выборочную дисперсию. Выборочным средним
Выборочное среднее называют также выборочным математическим ожиданием. Оно характеризует положение распределения случайной величины на оси x. Если данные представлены в виде вариационного ряда, то целесообразно для вычисления выборочного среднего использовать одно из следующих соотношений: · для дискретного вариационного ряда
· для интервального вариационного ряда
где
Пример. Вычислим значение выборочного среднего
К другим характеристикам положения распределения случайной величины относятся медиана Ме и мода Мo. Медиана (Ме) - среднее (серединное) значение вариационного ряда. · при четном числе вариант – · при нечетном числе вариант – где Медиана делит совокупность на две равные части. Ее приближенное значение можно получить по графику распределения. Мода (Мo) - наиболее часто встречающееся значение наблюдения. Мода имеет большое практическое значение. Она находит отражение при планировании производства товаров, при их распределении, при определении часов пик на станциях для оптимального планирования работы транспорта и т.д. В вариационных рядах близких к нормальному закону распределения медиана (Мe), мода (Мо), математическое ожидание М(х) (среднее арифметическое) практически совпадают по своим численным значениям.
Рис. 2.5.. Соотношение характеристик медиана Ме и мода Мo на графике плотности распределения вероятностей Для характеристики совокупности признака по необходимости применяют ряд других характеристик: квартили, децили, перцентили. Квартили – значение изучаемой величины, полученное при делении совокупности на четыре части, децили - на десять, перцентили - на сто частей. Дисперсия и среднеквадратическое отклонение являются характеристиками рассеяния или разброса распределения случайной величины, и чем больше разброс, тем сильнее варьируются значения случайной величины:
Число Если данные представлены в виде вариационного ряда, то целесообразно для вычислений · для дискретного вариационного ряда
· для интервального вариационного ряда
где
Рис. 2.6. Графики плотности распределения вероятностей с различными значениями дисперсии и одинаковыми математическими ожиданиями Выборочная дисперсия обладает одним существенным недостатком: если среднее арифметическое выражается в тех же единицах, что и значения случайной величины, то, как следует из формул, задающих дисперсию, последняя выражается уже в квадратных единицах. Этого недостатка можно избежать, взяв, в качестве меры рассеивания, арифметический квадратный корень из дисперсии. Выборочным средним квадратическим отклонением называется арифметический квадратный корень из выборочной дисперсии (обозначение σв). Пример. Используя выборку первого примера, вычислим значение выборочной дисперсии. Первоначально, используя дискретный вариационный ряд (пример о телефонной станции), получим
Так как значение
В качестве характеристики формы распределения, отражающей его асимметрию, служит коэффициент асимметрии (Аs иногда обозначается β; i), который рассчитывается по формуле:
Коэффициент асимметрии Аs изменяется в пределах (
Рис. 2.7. Зависимость формы плотности распределения вероятности от коэффициента асимметрии Неприведенный коэффициент эксцесса Ех также является характеристикой формы распределения, а именно его островершинности, и определяется из выражения
Неприведенный коэффициент эксцесса Ех изменяется в пределах
Рис. 2.8. Зависимость формы плотности распределений вероятности от приведенного коэффициента эксцесса γ
§ 3. Законы распределения выборочных характеристик После получения вариационного ряда как выборочного распределения возникает первая задача – найти на основе этого распределения общий закон распределения для данного признака. На основе всестороннего анализа имеющегося распределения и изучения рассматриваемого признака выбирают из известных распределений определенный закон распределения в качестве предполагаемого теоретического закона распределения для рассматриваемого признака в генеральной совокупности. Рассмотрим несколько распределений, которые имеют важные статистические приложения: · нормальное распределение, · c2 -распределение (распределение Пирсона), · t -распределение (распределение Стьюдента), · F -распределение (распределение Фишера). а) Нормальный закон распределения случайной величины. Нормальное распределение рассмотрено впервые А. Муавром в I733 г., а в I809 г. открыто независимо от исследований А. Муавра К. Гауссом. Распределение Муавра - Лапласа - Гаусса занимает ведущее место в теории и практике вероятностно-статистических исследований. Как уже было введено в разделе «Теория вероятностей», нормальным называется распределение, имеющее вид:
По этой формуле при различных значениях среднего арифметического ( Для нормального распределения значения моды, медианы и среднего арифметического равны между собой. При решении статистических задач во многих случаях применяется стандартное нормальное распределение (единичное, нормальное). Оно получается при усл
|

 .
.
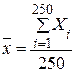 годовых доходов выбранных 250 жителей не более чем на 1000 руб., если известно, что среднее квадратичное отклонение годового дохода не превышает 2500 руб.
годовых доходов выбранных 250 жителей не более чем на 1000 руб., если известно, что среднее квадратичное отклонение годового дохода не превышает 2500 руб. , получаем
, получаем .
. .
. . Речь идет лишь о вероятности того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. Разница заключается в следующем: при обычной сходимости, рассматриваемой в математическом анализе, для всех п, начиная с некоторого значения, неравенство
. Речь идет лишь о вероятности того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. Разница заключается в следующем: при обычной сходимости, рассматриваемой в математическом анализе, для всех п, начиная с некоторого значения, неравенство  выполняется всегда; в нашем случае могут найтись такие значения п, при которых это неравенство неверно. Этот вид сходимости называют сходимостью по вероятности.
выполняется всегда; в нашем случае могут найтись такие значения п, при которых это неравенство неверно. Этот вид сходимости называют сходимостью по вероятности.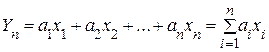 ,
,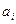 постоянные, фиксированные числа. Каждая i-ая случайная величина имеет
постоянные, фиксированные числа. Каждая i-ая случайная величина имеет  и
и 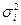 (i=1,2,3,…,n-1,n) =>
(i=1,2,3,…,n-1,n) =>  ,
,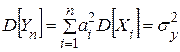 .
.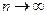 стремится к нормальному распределению
стремится к нормальному распределению 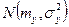 .
. - мерной случайной величины (X1, X2, X3,………Xn).
- мерной случайной величины (X1, X2, X3,………Xn).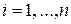 ).
). (
(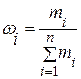 .
.

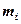
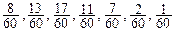
 ,
, ,
,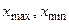 – наибольшее и наименьшее значения случайной величины. Величина (
– наибольшее и наименьшее значения случайной величины. Величина ( ) – называется размахом ряда. Если при вычислении h необходимо округлить результат, следует помнить, что последний интервал группирования будет меньше ширины h при округлении в большую сторону и больше h при округлении в меньшую сторону. При этом необходимо выполнение условий:
) – называется размахом ряда. Если при вычислении h необходимо округлить результат, следует помнить, что последний интервал группирования будет меньше ширины h при округлении в большую сторону и больше h при округлении в меньшую сторону. При этом необходимо выполнение условий: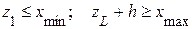 .
. ,
,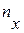 – количество элементов выборки меньших х. Другими словами,
– количество элементов выборки меньших х. Другими словами, 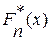 есть относительная частота появления события
есть относительная частота появления события  в
в 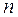 независимых испытаниях. По теореме Бернулли относительная частота появления события
независимых испытаниях. По теореме Бернулли относительная частота появления события 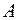 в
в  независимых испытаниях сходится при увеличении
независимых испытаниях сходится при увеличении 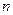 к вероятности
к вероятности  этого события. Следовательно, при больших объемах выборки выборочная функция распределения
этого события. Следовательно, при больших объемах выборки выборочная функция распределения 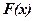 . Главное различие между
. Главное различие между  и
и  состоит в том, что
состоит в том, что 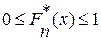 ;
;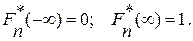



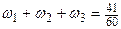

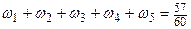



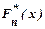
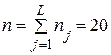 .
.



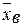 называется случайная величина, определяемая формулой
называется случайная величина, определяемая формулой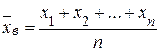 .
.
 ;
;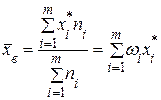 ,
,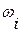 – частость (относительная частота), соответствующая i -й варианте или i -му частичному интервалу;
– частость (относительная частота), соответствующая i -й варианте или i -му частичному интервалу;  – середина i -го частичного интервала, т.е.
– середина i -го частичного интервала, т.е.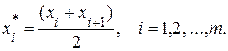
 по выборке примера о телефонной станции:
по выборке примера о телефонной станции: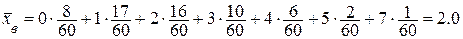 .
.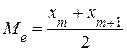 ,
,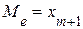 ,
,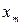 и
и 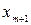 серединные значения.
серединные значения.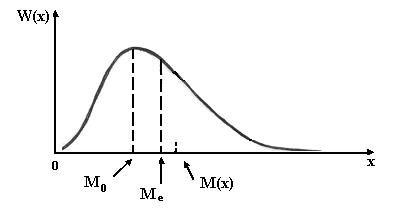
 .
. , полученное для отдельной выборки, является одним из значений случайной величины, которая называется выборочной дисперсией.
, полученное для отдельной выборки, является одним из значений случайной величины, которая называется выборочной дисперсией.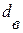 использовать одно из следующих соотношений:
использовать одно из следующих соотношений: ;
; ,
,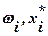 – те же, что и в предыдущих формулах.
– те же, что и в предыдущих формулах.
 .
.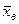 было уже вычислено ранее (
было уже вычислено ранее (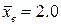 ), то по формуле для вычисления дисперсии получим:
), то по формуле для вычисления дисперсии получим: .
.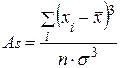 .
.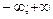 ). Для симметричного распределения Аs равен 0. Например, для модели нормального распределения Аs = 0. При Аs < 0 распределение имеет левостороннюю асимметрию, при Аs > 0 – правостороннюю. Например, правосторонняя асимметрия характеризуется тем, что середина ряда сдвинута влево от вершины распределения, т.е. частоты сначала быстро возрастают, а, достигнув наибольшего значения, в дальнейшем убывают значительно медленнее. Аналогично определяется левосторонняя асимметрия.
). Для симметричного распределения Аs равен 0. Например, для модели нормального распределения Аs = 0. При Аs < 0 распределение имеет левостороннюю асимметрию, при Аs > 0 – правостороннюю. Например, правосторонняя асимметрия характеризуется тем, что середина ряда сдвинута влево от вершины распределения, т.е. частоты сначала быстро возрастают, а, достигнув наибольшего значения, в дальнейшем убывают значительно медленнее. Аналогично определяется левосторонняя асимметрия.
 .
. . Для нормального распределения Ех =0. Величина γ = Ех -3 называется приведенным коэффициентом эксцесса.
. Для нормального распределения Ех =0. Величина γ = Ех -3 называется приведенным коэффициентом эксцесса.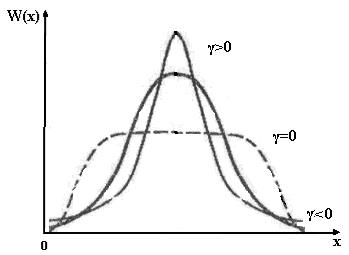
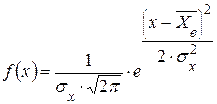 .
.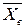 ) и среднеквадратичного отклонения (
) и среднеквадратичного отклонения (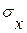 ) получается семейство нормальных кривых. Нормальное распределение симметрично относительно
) получается семейство нормальных кривых. Нормальное распределение симметрично относительно  и имеет следующие числовые характеристики: математическое ожидание a=
и имеет следующие числовые характеристики: математическое ожидание a=  , коэффициент асимметрии Аs=0, неприведенный коэффициент эксцесса Ех = 3, приведенный коэффициент эксцесса γ = 0.
, коэффициент асимметрии Аs=0, неприведенный коэффициент эксцесса Ех = 3, приведенный коэффициент эксцесса γ = 0.


