Методы регрессионного и корреляционного анализа 2 страница
Вариант 3 1. В группе 35 студентов. Они обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек? 2. Эксперимент состоит в том, что вытаскивают две кости домино по очереди. Событие A - на первой из костей очков больше, чем на второй. Придумайте такие события, которые вместе с событием A образовывали бы полную группу событий. 3. Карточки, на которых написаны буквы "р", "а", "д", "о", "с", "т", "ь", раскладывают в ряд в случайном порядке. Найдите вероятность того, что при этом слово «радость» не сложится. 4. Есть две монеты - одна правильная (с вероятностью выпадения "герба" 1/2), а другая фальшивая (с вероятностью выпадения «герба» 2/3). Проделывают следующий опыт: сначала бросают правильную монету, если выпал "герб", то правильную монету бросают еще раз, а если «решетка», то бросают фальшивую монету. Найти вероятность того, что всего выпадет 1 «герб». 5. Одновременно бросают игральную кость и монету, если на монете выпал «герб», то к сумме очков на кости прибавляют 2. Найти распределение, среднее и дисперсию числа очков, выпавших в результате эксперимента. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. Для проведения градостроительных работ вся территория изучаемого района была разделена на 50 сравнительно одинаковых районов и подсчитано количество жителей, проживающих в этих районах. Результаты опроса приведены ниже. Составить вариационный ряд. Определить статистические характеристики ряда. Построить полигон, гистограмму, кумуляту, огиву ряда. Дать объяснение полученным характеристикам. 2. При обслуживании 200 автомашин в авторемонтной мастерской стоимость разных услуг в среднем составила 800 рублей. В каких размерах может варьировать стоимость услуг с вероятностью 0,98% при среднеквадратическом отклонении 500 рублей. 3. В условиях задачи № 1 проверить гипотезу о нормальном распределении ряда. 4. Для изготовления детали норма предусматривает 30 минут. Однако рабочий тратит на выполнение заказа больше времени. Проверка работы у 15 рабочих определила среднее время изготовления детали 35 минут. На уровне значимости α = 0,01 определить, можно ли утверждать, что среднее время соответствует норме, если исправленное выборочное отклонение s = 3,2 минуты. 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 4 1. На участие в команде претендует 10 мальчиков и 5 девочек. Сколькими способами можно сформировать команду, состоящую из трех мальчиков и двух девочек? 2. Эксперимент состоит в том, что из колоды карт вынимают две карты. Событие A - вынули одну карту красной масти. Придумайте такие события, которые вместе с событием A образовали бы полную группу событий. 3. На карточках написаны буквы, входящие в слово "параллелепипед". По очереди берут две карточки. Найти вероятность того, что на первой карточке гласная, а на второй согласная. 4. На елке детям дарят зайцев и мишек - зайцев 40%, а мишек 60%. Среди зайцев 70% серого цвета, остальные белого, а среди мишек 60% коричневые, а остальные тоже белые. Ребенку досталась игрушка белого цвета. Найти вероятность того, что это заяц. 5. В ящике 3 белых и 5 черных шариков. Из ящика последовательно извлекают 4 раза по одному шарику и запоминают его цвет (каждый раз шарик возвращают обратно). Найти распределение, среднее и дисперсию числа белых шариков. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. В течении двух месяцев (60 дней) на одной автомобильной стоянке численность иномарок по ежедневным подсчетам составило Построить вариационный ряд, гистограмму, диаграмму, огиву, найти характеристики ряда и дать объяснение полученным результатам. 2. Банк, изучая возможности предоставления кредитов, сделал опрос населения с целью определения среднего размера кредита. Было опрошено500 человек из 4000. Среднее значение суммы составило 3000 рублей с отклонением 800 рублей. Найти границы 95%-го доверительного интервала для оценки неизвестного среднего размера кредита. 3. В условиях задачи № 1 проверить гипотезу о нормальном распределении ряда. 4. Экономический анализ производительности труда позволил поставить гипотезу о наличии 2-х типов предприятий с различной средней величиной показателя производительности труда. Выборки 50 предприятий первого типа дала результат - средняя производительность равна 120 деталей и 60 предприятий второго типа - средняя производительность 111 деталей. Генеральные дисперсии известны Д(I)=126, Д(II)=130. На уровне значимости 0,05 проверить случайно ли полученное различие, т.е. Но: равенство генеральных средних; Н1:неравенство генеральных средних. 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 5 1. Три пары хотят пойти в театр. Им предложили в кассе театра 4 билета рядом на 1-м ряду, 4 билета рядом на 4-м ряду и 6 билетов рядом на 5-м ряду. Сколько существует вариантов, если они рассаживаются парами? 2. Событие A состоит в том, что студент увлекается спортом, событие C - студент участвует в художественной самодеятельности. Запишите событие, состоящее в том, что студент увлекается спортом и участвует в художественной самодеятельности. Что означает событие A+C? 3. В урне 5 белых и 6 черных шаров. Вынимаются одновременно два шара. Какова вероятность того, что они разноцветны? 4. Завод использует детали, поступающие с трех фабрик. При этом первая фабрика поставляет 30% деталей, вторая - 50%, а третья - 20%. По дороге с первой фабрики портится 20% деталей, со второй - 10%, а с третьей - 40%. Найти вероятность того, что случайно выбранная деталь окажется испорченной. 5. В ящике 4 белых и 6 черных шариков. Достают четыре шарика. Найти распределение, среднее и дисперсию числа белых шариков. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. При выяснении темпа роста курса акций по сравнению с предыдущим месяцем были опрошены 50 представителей различных фирм. Результаты опроса приведены в процентах:
Составить вариационный ряд. Определить статистические характеристики. Построить гистограмму, полигон, кумуляту, огиву. Дать объяснение полученным характеристикам. 2. Агентство недвижимости занималось подбором квартир для расселения жильцов многоквартирного дома. Оказалось, что в среднем для 50 семей необходимая затрата составит 29000 у.е. Определить доверительный интервал стоимости квартир с надежностью 95% при неизвестном среднеквадратическом отклонении и при условии, что распределение нормальное. 3. Проверить гипотезу о нормальном распределении по условию задачи №1. 4. Вес одной конфеты в упаковке должен быть 10 грамм. Выборочная проверка 120 конфет показала, что средний вес равен хср = 12,5. Требуется при уровне значимости α = 0,01 проверить гипотезу Н0 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 6 1. Три человека едут в Москву. В кассе осталось 10 билетов, из них 2 на 23 поезд, 3 на 27 поезд, а 5 на 25 поезд. В каких составах они могут поехать. 2. Эксперимент состоит в том, что одновременно бросают игральную кость и монету. Событие A - выпало нечетное число и герб. Придумайте такие события, которые вместе с событием A образовывали бы полную группу событий. 3. Найдите вероятность того, что у произвольно выбранного пятизначного числа первая цифра больше последней. 4. Игральную кость бросают 8 раз. Что вероятнее: выпадение четного числа 5 раз или выпадение "тройки" не более одного раза. 5. Шахматист А держит пари, что выиграет хотя бы одну партию из 5 у шахматиста В. Вероятность выиграть для А в каждой партии равна 0.4. Шахматисты заканчивают свой матч после первой победы шахматиста А, но играют не более 5 партий. Найти распределение и среднее значение числа партий, которые проиграл А. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. На определенном участке шоссе по подсчетам ГИБДД в течении года произошло 50 дорожно-транспортных происшествий. Количество пострадавших в них составило Построить вариационный ряд, гистограмму, полигон, огиву, кумуляту. Найти характеристики ряда. Дать объяснение полученным результатам. 2. Опрос 120 общественных организаций в некотором городе дал сведения, что только 75 из них занимаются благотворительной деятельностью, направленной на осуществление программы "Здоровый образ жизни". Построить доверительный интервал с 95% оценивающий среднее количество организаций, чьи интересы направлены на молодежную политику при S = 80. 3. В условиях задачи № 1 проверить гипотезу о нормальном распределении. 4. Главный бухгалтер большой компании, объединяющей несколько маленьких фирм, при обследовании обнаружил неправильно оформленные счета. Из 1500 выбранных 35 оказалось неверными. Год спустя при проверке в порядке случайного отбора он проверил 2000 счетов, и 30 из них оказались неверными. Можно ли утверждать, что число неверных счетов уменьшилось? Принять уровень значимости 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 7 1. Музыкальный концерт состоит из трех песен и двух скрипичных пьес. Сколько существует способов составления программы концерта так, чтобы он начинался исполнением пьесы? 2. Событие A означает, что мальчику подарили машину, событие B - подарили велосипед, событие C - подарили трактор. Запишите события, состоящие в том, что: a) подарили велосипед и еще какую-то технику (машину или трактор); b) подарили машину и трактор, но не подарили велосипед. 3. В кошельке 8 монет - 1 монета достоинством в 20 коп., 4 монеты по 15 коп., 3 монеты по 5 коп. Наугад вынимают 2 монеты. Найдите вероятность того, что в сумме будет меньше 21 коп. 4. Компьютерная игра состоит из трех партий. Некто, играя в эту игру побеждает в партиях с вероятностью 0.5, 0.3 и 0.1 соответственно. Найти вероятность того, что некто победит, если победа зачитывается в том случае, если выиграны по крайней мере две партии, одна из которых последняя. 5. Два баскетболиста поочередно бросают мяч в корзину. Игра продолжается до тех пор, пока один из игроков не промахнется. Вероятность попадания в корзину для каждого игрока 0.8. Найти распределение числа бросков. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. На грандиозном фестивале, на острове Ибица собралось 50 ди-джеев из разных стран. Количество пластинок, привезенных ими на фестиваль, составило ряд Построить вариационный ряд, гистограмму, полигон, огиву, кумуляту. Определить статистические характеристики ряда. Дать объяснение полученным результатам. 2. С целью изучения размеров дневной выручки торговых ларьков было опрошено 100 владельцев. В результате опроса выяснилось, что средняя выручка составила 300 д.е. В каких пределах с вероятностью 0,95 может оказаться дневная выручка, если среднеквадратическое отклонение составило 100 д.е. 3. В условиях задачи № 1 проверить гипотезу о нормальном распределении. 4. По данным 12 рейсов установлено, что в среднем машина затрачивает на поездки от завода до хлебоприемного пункта 73 минуты. Допустив, что время поездки - нормальная случайная величина, проверить гипотезу 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 8 1. На тарелке лежит 5 яблок и 4 груши. Сколькими способами можно отобрать 4 фрукта, чтобы среди них были и яблоки, и груши. 2. Событие A состоит в том, что девочке подарили куклу, а событие B - ей подарили мяч, событие C - ей купили мороженое. Что означают события: a) A+ B C b) A B C? 3. В игре принимают участие 10 мальчиков и 12 девочек. Двоих водящих выбирают по очереди. Найти вероятность того, что оба водящих мальчики. 4. В одном ящике 3 белых и 5 черных шариков, а в другом 4 белых и 4 черных шарика. Бросают монету, если выпал "герб" извлекают шарик из первого ящика, а иначе - из второго. Найти вероятность того, что извлекли белый шарик. 5. Игральная кость бросается 2 раза. Найти распределение и среднее значение произведения выпавших очков. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. При покупке компьютера организация провела тендер. Были получены следующие данные о стоимости компьютеров (в долларах) Составить вариационный ряд. Определить статистические характеристики. Построить полигон, гистограмму, кумуляту, огиву. Дать объяснение полученным результатам. 2. У 100 обезьян при проверке содержания кальция в организме оказалось в среднем равно 11,94 мг при среднеквадратическом отклонении 1,26. Установить доверительный интервал, в котором с вероятностью р=0,095 должна находиться генеральная средняя. 3. В условиях задачи № 1 проверить гипотезу о нормальном распределении. 4. Фирма торгующая товаром утверждает, что покупатели охотно покупают их товар. Случайная выборка показала что, только 30 человек из 200 предпочитают этот товар. Другая фирма конкурент также утверждает, что их товар лучше покупается. Она отобрала группу из 300 человек и только 25 из них покупают этот товар. Приняв уровень значимости 5. Построить корреляционное поле связи между (Y) и (X). Сделать предварительный вывод о характере связи. Определить параметры уравнения парной регрессии и коэффициент корреляции.
Вариант 9 1. Каким количеством способов можно выбрать двух человек из 6 кандидатов на две различные должности? 2. Событие А состоит в том, что мальчику подарили паровоз, событие В - подарили машину, событие С - мальчика повели в кино. Запишите событие, состоящее в том, что мальчику подарили обе игрушки, но не сводили в кино. Что означает событие (А+В)С? 3. Технический контроль проверяет партию в n=10 изделий. Для этого выбирается наугад m =3 изделия. Известно, что во всей партии имеется k=4 изделия с браком. Какова вероятность того, что среди проверяемых изделий будет обнаружено ровно l=2 бракованных изделия? 4. Завод получает 60% деталей с одной фабрики (10% брак) и 40% с другой (5% брак). Наугад выбранная деталь оказалась бракованной. Найти вероятность того, что она изготовлена на первой фабрике. 5. Баскетболист бросает мяч в корзину до первого промаха, но не более 6 раз. Вероятность промаха 0.1. Найти распределение и среднее значение числа удачных бросков. 6. Известна интегральная функция распределения
Требуется вычислить математическое ожидание и дисперсию, построить графики интегральной и дифференциальной функций. ________________________________________________________________ 1. Результаты измерения давления у больного записывались ежедневно в журнале. Составить вариационный ряд. Определить статистические характеристики. Построить гистограмму, полигон, кумуляту, огиву. Дать объяснение полученным характеристикам. 2. Служба контроля по использованию воды с целью установки счетчиков провела выборочную проверку в одном многоквартирном доме. Было отобрано 10 квартир. Расход воды составил (кубм3)
С вероятностью 0, 95 определить доверительный интервал для оценки среднего расхода воды на 1 квартиру при условии, что в доме 120 квартир. 3. В условиях задачи № 1 проверить гипотезу о нормальном распределении. 4. Произведен стандартный тест для выяснения неких способностей. В изданном тексте утверждается, что принятая средняя
|



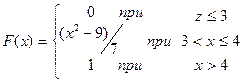 .
.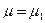 при конкурирующей
при конкурирующей 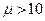 .
.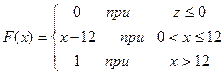
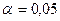 .
.
 мин. при конкурирующей
мин. при конкурирующей 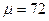 , если выборочное среднеквадратическое отклонение равно S = 4 мин.
, если выборочное среднеквадратическое отклонение равно S = 4 мин.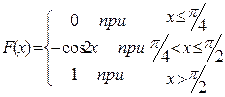 .
.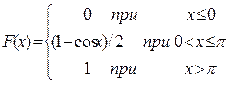 .
. и стандартное отклонение
и стандартное отклонение 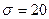 . Полученная выборочная средняя
. Полученная выборочная средняя  . При уровне значимости 0,05 определить насколько выборка из 62 человек соответствует всей генеральной совокупности.
. При уровне значимости 0,05 определить насколько выборка из 62 человек соответствует всей генеральной совокупности.


