Решение. Для вычисления дисперсии составим закон распределения X2: X2 P(X) 0.2 0.3 0.5
M(X)=1×0.2+2×0.3+3×0.5=2.3. Для вычисления дисперсии составим закон распределения X2:
M(X2)=1×0.2+4×0.3+9×0.5=5.9. è Такая характеристика случайной величины, как математическое ожидание, называется иногда характеристикой положения, так как она дает представление о положении случайной величины на числовой оси. Другими характеристиками положения являются мода и медиана. Модой М0[X] называется значение случайной величины Х, при котором плотность распределения f (x) имеет наибольшее значение – для непрерывной случайной величины, а для дискретной – мода это значение случайной величины, соответствующее большей вероятности. Медианой Ме [ X ] непрерывной случайной величины Х, называют ее значение, определяемой равенством
или
Для случайных величин существует несколько наиболее распространенных распределений, характеристики которых приведены в таблице. Сводная таблица характеристик законов распределения дискретных случайных величин
Сводная таблица характеристик законов распределения непрерывных случайных величин
Обратим особое внимание на нормально распределенные случайные величины. В 1718 в Лондоне вышла в свет книга французского математика А.Муавра (1667-1754) «Учение о случаях». Он открыл закономерность, которая часто наблюдается в случайных явлениях, теоретически обосновал роль «нормального» распределения. А.Муавр измерил рост у 1375 случайно выбранных женщин. Колоколообразная кривая (см. рисунок 3.1), которая приближенно «накрывает» диаграмму распределения роста, близка к графику функции
где
Рис. 3.1. Распределение показателя роста В общем случае для нормального закона Пример. Случайная величина X распределена по нормальному закону
Найти P(-3<X<3). Решение. По свойству функции распределения имеем P(-3<X<3)=F(3)-F(-3)=
= Этот интеграл не вычисляется в элементарных функциях, его численное значение находится по таблицам (см.приложение). Так как
то следует
где a и s – параметры нормального закона. Таким образом, для данного примера получаем:
Закон нормального распределения имеет важное практическое значение. Множество величин на практике имеют нормальное распределение. Например, распределение приращений индексов развитых стран, курсы акций, распределение веса новорожденных, скорости газовых молекул и т.д. Для этих величин характерным является то, что на их формирование влияет большое число факторов, причем влияние каждого из них мало и ни один фактор не имеет значительного преимущества перед другими. При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
Если принять D = 3s, то по таблицам значений функции Лапласа находим, что
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину большую, чем утроенное среднее квадратичное отклонение, практически равна нулю. Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение. Замечание. Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8, 2,9 или 3,2 и получить тот же вероятностный результат. Учитывая, что Ф (2)=0,477, можно было бы говорить и о правиле двух сигм. Пример. Поезд состоит из 100 вагонов. Масса каждого вагона – случайная величина, распределенная по нормальному закону с математическим ожиданием а = 65 т и средним квадратичным отклонением s = 0,9 т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется. Решение. Второй локомотив не потребуется, если отклонение массы состава от ожидаемого (100×65 = 6500) не превосходит 6600 – 6500 = 100 т. Т.к. масса каждого вагона имеет нормальное распределение, то и масса всего состава тоже будет распределена нормально. Получаем:
На практике для проверки распределения на нормальность обычно используют анализ гистограммы, нормальные вероятностные графики или численные методы оценки коэффициентов асимметрии и эксцесса; критерий Пирсона (χ-квадрат). Эти методы будут рассмотрены далее.
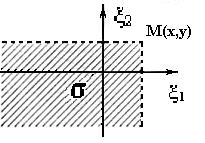
§ 4. Двумерные случайные величины Часто приходится решать задачи, в которых рассматриваются события, описываемые не одной, а несколькими, в частности, двумя случайными величинами. Наряду с одномерными случайными величинами, возможные значения которых определяются одним числом, теория вероятностей рассматривает и многомерные случайные величины. Каждое возможное значение такой величины представляет собой упорядоченный набор нескольких чисел. Геометрической иллюстрацией этого понятия служат точки п -мерного пространства, каждая координата которых является случайной величиной (дискретной или непрерывной), или п -мерные векторы. Поэтому многомерные случайные величины называют еще случайными векторами. Например, в задаче «о встрече» время прихода одного участника (ξ) и другого (ή), если условия их прихода известны (скажем - любой момент в течение заданного часа), пару чисел ξ, ή можно рассматривать как двумерную случайную величину. Двумерной случайной величиной называется система из двух случайных величин (ξ, ή), для которой определена вероятность Функцией распределения F(x, y) двумерной случайной величины (ξ,ή), называется вероятность совместного выполнения неравенств ξ1<x и ή<y, где x и y - любые действительные числа: F (х, у) = Рассмотрим ξ и ή как декартовы координаты точки на плоскости. Точка М(ξ, ή) может занимать то или иное положение на плоскости 0ξή;. Тогда функция распределения даст вероятность того, что случайная точка М(ξ, ή) попадает в область σ;, изображенную на рис.4.1.
Рис. 4.1. Область функции распределения Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины. Двумерная случайная величина (ξ, ή) называется дискретной, если ξ и ή дискретные величины. Пусть возможные значения ξ и ή образуют, например, конечные последовательности x1, x2,..., xn и y1, y2,..., ys. Возможные значения двумерной случайной величины (ξ, ή) имеют вид (xi, yj), где i=1, 2,..., n; j=1, 2,..., s. Обозначим через pij вероятность того, что (ξ, ή) =(xi,yj):
В этом случае функция распределения F(х, у) имеет вид
где двойная сумма распространена на те i и j, для которых xi<x и yj<y. Закон распределения дискретной двумерной случайной величины (ξ,ή), так же, как и одномерной, можно задать таблицей. Первая строка таблицы содержит возможные значения случайной величины ξ, а первый столбец — возможные значения ή. В остальных клетках таблицы указаны соответствующие вероятности. При этом сумма вероятностей, стоящих во всех клетках таблицы, равна 1. Зная закон распределения двумерной случайной величины, можно найти законы распределения ее составляющих, так как событие Х = х 1 представляет собой сумму несовместных событий (X = x 1, Y = y 1), (X = x 1, Y = y 2),…, (X = x 1, Y = ym), поэтому р (Х = х 1) = p (x 1, y 1) + p (x 1, y 2) +…+ p (x 1, ym) (в правой части находится сумма вероятностей, стоящих в столбце, соответствующем Х = х 1). Так же можно найти вероятности остальных возможных значений Х. Для определения вероятностей возможных значений Y нужно сложить вероятности, стоящие в строке таблицы, соответствующей Y = yj. Две дискретные случайные величины ξ и ή называются независимыми, если закон распределения одной из них не зависит от того, какое значение принимает другая случайная величина, то есть если для всех пар i, j выполняется соотношение
Пример. Задано распределение вероятностей дискретной двумерной случайной величины (X;Y):
Составить законы распределения её компонент
|

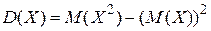 =5.9-(2.3)2=0.61.
=5.9-(2.3)2=0.61.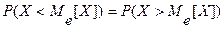
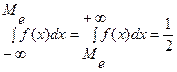 .
.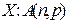
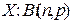
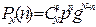
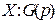
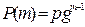
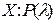
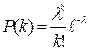
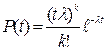
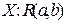
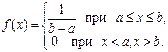

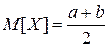 ,
, 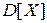 =
=  ,
, 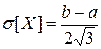 .
.
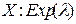
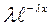 F(x)=
F(x)= 
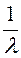 , D [ X ]=
, D [ X ]= 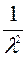 , σ;[ X ]=
, σ;[ X ]= 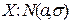
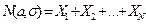 где
где 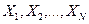 – большое число независимых в совокупности случайных величин, воздействие каждой из которых на
– большое число независимых в совокупности случайных величин, воздействие каждой из которых на  равномерно незначительно и равновероятно по знаку (согласно центральной предельной теореме)
равномерно незначительно и равновероятно по знаку (согласно центральной предельной теореме)
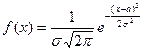 F(x)=
F(x)= 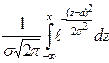
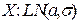
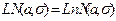
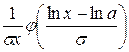 ,
F(x)=
,
F(x)= 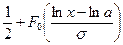
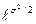 , D [ X ]=
= a
, D [ X ]=
= a 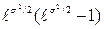
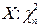
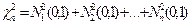 где
где 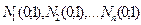 — независимые в совокупности случайные величины
— независимые в совокупности случайные величины
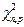 , соответствующие вероятности
, соответствующие вероятности
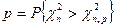 , приведены в таблице, при
, приведены в таблице, при 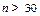
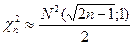
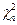 )=n,
D(
)=n,
D(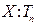
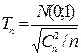 , где N(0;1) и
, где N(0;1) и 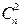 — независимые случайные величины
— независимые случайные величины
 , соответствующие вероятности
, соответствующие вероятности 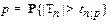 , приведены в таблице, при
, приведены в таблице, при 
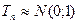
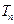 )=0,
D(
)=0,
D(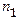 и
и 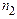 степенями свободы
степенями свободы
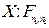
 , где
, где 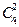 и
и 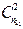 — независимые случайные величины
— независимые случайные величины
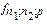 , соответствующие вероятности
, соответствующие вероятности  , приведены в таблице
, приведены в таблице
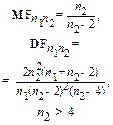
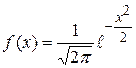 ,
,

 , где
, где 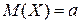 . Дисперсия же вычисляется по формуле
. Дисперсия же вычисляется по формуле 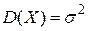 .
.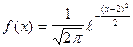 .
.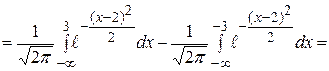
 .
.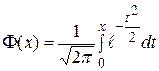 ,
,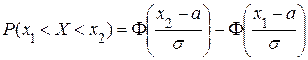 ,
,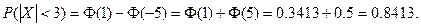
 .
. .
.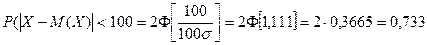 .
.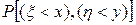 совместного выполнения неравенств ξ<x и ή <y, где x и y - любые действительные числа.
совместного выполнения неравенств ξ<x и ή <y, где x и y - любые действительные числа.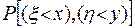
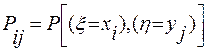 .
. ,
,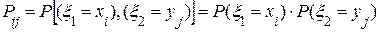 .
. и
и  . Определить вероятность P{X<Y}.
. Определить вероятность P{X<Y}.


