По изучению курса высшей математики
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Санкт-Петербургский государственный университет сервиса и экономики Кафедра «Математика и математические методы в экономике» Элементы теории вероятностей и математической статистики Учебное пособие по изучению курса высшей математики Санкт-Петербург Одобрено на заседании кафедры «Математика и математические методы в экономике» протокол № __ от __.__.2006г. Утверждены Методическим советом ИЭУПС протокол № __ от __.__.2006 г.
Учебное пособие охватывает основные разделы курса теории вероятностей и математической статистики. Данный курс читается студентам Университета Сервиса и Экономики. Пособие соответствует требованиям Государственного образовательного стандарта к профессиональным образовательным программам по всем специальностям дневной и заочной форм обучения. В учебном пособии излагаются основные понятия и методы, необходимые для анализа данных; на отдельных примерах рассматриваются постановки задач и их решение. Оно может быть использовано для первого знакомства с методами теории вероятностей и математической статистики. Пособие дает представление об основных статистических методах, их возможностях и границах применения. Внимательное ознакомление с данным методическим пособием поможет при выполнении контрольных заданий по теории вероятностей и математической статистике, так как разнообразные примеры в какой-то степени аналогичны задачам контрольных работ. Задания для контрольной работы представлены в конце пособия. Большинство задач по каждой теме иллюстрирует применение математических методов при исследовании экономических, социальных и т.д. процессов, при принятии управленческих решений. В процессе решения таких задач студент не только закрепляет и углубляет теоретические знания, полученные на лекциях, но и учится применять эти знания при постановке и решении конкретных практических задач. В приложении к пособию приведен ряд таблиц, необходимых для выполнения контрольных работ.
Составители: В.Б. Дворяшин, к.ф.-м.н., доцент Н.Ю.Кропачева, к.ф.-м.н., доцент Г.А.Петросян, ст.преподаватель
Рецензенты: профессор кафедры МиММЭ СПбГУСЭ д. ф.-м.н. А.И.Шерстюк доцент кафедры общей математики и информатики математико-механического факультета СПбГУ к. ф.-м.н. Г.В.Павилайнен
Ó Санкт-Петербургский государственный университет 2007 г. Содержание
Что ни толкуй Вольтер или Декарт Мир для меня - колода карт, Жизнь - банк; рок мечет, я играю, И правила игры я к людям применяю. М. Ю. Лермонтов
Замечательно, что наука, которая началась с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания... Ведь по большей части важнейшие жизненные вопросы являются на самом деле лишь задачами из теории вероятностей. П.Лаплас Введение В своей практической деятельности мы часто встречаемся с явлениями, исход которых нельзя предсказать. Например: нельзя определить однозначно результат выпадения «орла» или «решки» в результате подбрасывания монеты, но при многократном подбрасывании выпадает примерно одинаковое число «орлов» и «решек». Изучение количественных закономерностей, которым подчиняются массовые случайные события, и составляет предмет теории вероятностей. В основе этой теории лежат специальные математические модели, в которых сопоставлению событий по степени их правдоподобия можно придать точный смысл. Впервые основы теории вероятностей были изложены последовательно французским математиком П.Лапласом (1749-1827) в книге «Аналитическая теория вероятностей». Для решения задач, связанных с анализом информации при наличии фактора случайности, разработана совокупность методов, которая называется математической статистикой. Математическая статистика возникла в 17 веке и развивалась параллельно с теорией вероятностей. Между основными понятиями в математической статистике и теории вероятностей существует тесная взаимосвязь, которая обосновывает практическую ценность теории вероятностей и подтверждает теоретическую основу математической статистики. Общим для статистических и вероятностных характеристик является техника их вычислений. Главное различие между ними состоит в том, что статистические характеристики относятся к эмпирическим, а вероятностные к теоретическим понятиям. Статистические характеристики - это величины, которые при соблюдении определенных условий стремятся к вероятностным. Вероятностные характеристики можно рассматривать как предельные значения сопоставимых им характеристик математической статистики при возрастании числа наблюдений или опытов. Исследование математико-статистических моделей позволяет делать обоснованные выводы, решать задачи прогнозирования в различных сферах человеческой деятельности. Элементы комбинаторики В теории вероятностей часто приходится иметь дело с задачами, в которых необходимо подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Задачи такого типа называются комбинаторными, а раздел математики, занимающийся решением таких задач, — комбинаторикой. Иначе: комбинаторика изучает вопрос о том, сколько различных комбинаций подчиненных тем или иным условиям можно составить из конечного числа различных элементов, безразлично какой природы. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Пусть n - натуральное число. Через n! (читается «n-факториал») обозначается число, равное произведению всех натуральных чисел 1 от до n: n! = 1 * 2 * 3 *... * n. В случае если n=0, то по определению полагается: 0! = 1. Пример. Найдем значения следующих выражений: 1! = 1 2! = 1 * 2 = 2 3! = 1 * 2 * 3 = 6 4! = 1 * 2 * 3 * 4 = 24 5! = 1 * 2 * 3 * 4 * 5 = 120 6! = 1 * 2 * 3 * 4 * 5 * 6 = 720. Если n сравнительно велико (n>10),то часто n! вычисляют по формуле Стирлинга: Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок вычисляется по формуле:
Пример. Сколько различных десятизначных чисел можно составить из цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9? Решение. Так как каждая цифра в обозначении числа встречается один раз и цифра 0 не должна занимать первое место, то из 10 цифр можно составить 10! различных чисел, в которых каждая цифра содержится один раз, но из общего количества полученных чисел 9! чисел начинаются цифрой 0. Следовательно, искомое количество чисел равно: 10! – 9! = 9 × 9! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 92 = 3 265 920. Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений вычисляется по формуле:
|
Федеральное агентство по образованию
, где p = 3,14159..., е = 2,71828..., точность которой улучшается с увеличением n. Так при n=5 по приближенной формуле получаем 118,019. Относительная ошибка при этом составляет 2%.
, где n! =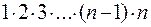 
.
.
