Классификация плоских механизмов по Л. В. Ассуру
Замечено, что к любому плоскому механизму можно присоединить такую кинематическую цепь, что степень его подвижности не изменится. Если эта цепь является кратчайшей (т.е. не распадается на более короткие и обладающие тем же свойством), и если при ее формировании использованы только низшие пары пятого класса, то такую цепь называют структурной группой или группой Ассура (в дальнейшем – просто группой). При наличии в механизме высших пар от них всегда можно избавиться с помощью описанной выше процедуры замены. Из сказанного следует, что группа, присоединенная к стойке, имеет нулевую подвижность, но тогда она является и кинематически и статически определимой системой. Пусть группа состоит из n звеньев; для соединения этих звеньев между собой и для присоединения группы к стойке или к подвижным звеньям механизма использовано
или
Из (1.3) заключаем, что группа может состоять только из четного числа звеньев, число пар пятого класса в группе всегда в полтора раза больше числа звеньев. Те пары, с помощью которых группа присоединяется к механизму, называют внешними, их количество определяет порядок группы; остальные пары, посредством которых звенья группы соединяются между собой, называют внутренними. После отсоединения от механизма всех структурных групп останется стойка и начальные звенья в количестве W (речь идет о фактической степени подвижности механизма, рассчитанной после исключения пассивных связей и местных подвижностей). Каждое начальное звено со стойкой называют начальным механизмом; таким образом, механизм состоит из W начальных механизмов и некоторого количества структурных групп, присоединенных в строго определенном порядке, который отражают в специальной записи, называемой формулой строения. Например, механизм с двумя степенями свободы, содержащий шесть структурных групп, может иметь такое строение
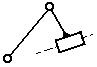
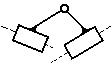
В зависимости от количества звеньев в группе и способа их соединения между собой группы делят на классы. Все двузвенные группы (
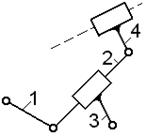
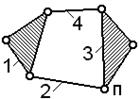
Класс групп, состоящих более чем из двух 1. В основе любого механизма лежит один или несколько начальных механизмов. Начальный механизм – это начальное звено со стойкой.звеньев, определяется числом вершин (или сторон) многоугольника, образуемого внутренними кинематическими парами на структурной схеме группы, которая строится по следующим правилам: · все вращательные и поступательные пары пятого класса изображают на этой схеме как вращательные; · звенья, участвующие в нескольких кинематических парах, изображаются в виде соответствующих многоугольников. На рис. 1.11 и 1.12 для удобства сопоставления помещены рядом друг с другом кинематические и структурные схемы двух групп различных классов.
На структурной схеме для большей наглядности можно те шарниры, которым на кинематической схеме соответствуют поступательные пары, помечать буквой «п». В структурных схемах групп III класса внутренние шарниры образуют один или несколько треугольников жесткой (неизменяемой) конфигурации; в схемах групп более высоких классов встречаются многоугольники (изменяемой конфигурации) с четырьмя и большим числом сторон, которое и определяет класс группы.
Отметим, что классификации Л. В. Ассура подчиняются только те плоские механизмы, у которых начальные звенья образуют кинематические пары со стойкой.
|

 пар пятого класса; тогда для группы, согласно (1.1), можно записать
пар пятого класса; тогда для группы, согласно (1.1), можно записать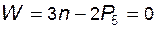 , (1.2)
, (1.2) . (1.3)
. (1.3)
 ) являются группами II класса второго порядка; дополнительно эти группы, в зависимости от количества поступательных пар, использованных при их формировании, делятся на виды (рис. 1.10).
) являются группами II класса второго порядка; дополнительно эти группы, в зависимости от количества поступательных пар, использованных при их формировании, делятся на виды (рис. 1.10).