Кинематический анализ механизма выполняется либо для заданного момента времени, либо для заданного положения входного звена; иногда для анализируемого положения механизма задают взаимное расположение каких-либо его звеньев.
Целью кинематического анализа механизма является:
1) Определение положений звеньев и каких-либо выбранных точек этих звеньев.
2) Определение скоростей и ускорений этих точек, а также угловых скоростей и угловых ускорений звеньев.
3) Изучение траекторий движения выбранных точек.
Исходными данными при анализе являются:
1) Кинематическая схема механизма.
2) Размеры и иные геометрические параметры звеньев (но только такие, которые не изменяются при движении механизма).
3) Законы движения входных звеньев (или параметры движения, например, угловая скорость и угловое ускорение входного звена в выбранном для анализа положении механизма).
Для механизмов, подчиняющихся классификации Л. В. Ассура, порядок кинематического анализа определяется формулой строения: вначале находят параметры движения начальных механизмов и затем – структурных групп в порядке следования их в формуле строения. Здесь следует руководствоваться простым правилом: кинематика любогоэлемента формулы строения может быть изучена только после того, как она изучена для всех предшествующих в этой формуле элементов.
Из множества применяемых методов анализа наиболее широко используют аналитические и графоаналитические методы. Из графо-аналитических методов в силу своей наглядности и простоты наиболее употребителен метод планов скоростей и ускорений, тем более что результаты графических построений нередко допускают их обработку точными аналитическими методами.
Теоретические основы метода планов
скоростей и ускорений
Векторный план – это графическое изображение векторного равенства. Построение плана всегда выполняется при строгом соблюдением длин и направлений векторов.
В основу кинематического анализа плоских механизмов положена теория плоскопараллельного движения твердого тела и теория сложного движения точки. В соответствии с этим рассмотрим два случая.
· Две точки A и B принадлежат одному звену, совершающему плоскопараллельное движение.
Скорости этих точек удовлетворяют формуле
 . (2.1)
. (2.1)
На рис. 2.1 изображен возможный вид плана скоростей по уравнению (2.1); здесь  –
–  полюс плана, в который помещают начала векторов абсолютных скоростей всех интересующих нас точек. Скорости
полюс плана, в который помещают начала векторов абсолютных скоростей всех интересующих нас точек. Скорости 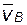 и
и 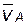 могут быть любыми, но концы этих векторов на плане обязательно находятся на одной прямой, перпендикулярной линии AB на звене, т.е.
могут быть любыми, но концы этих векторов на плане обязательно находятся на одной прямой, перпендикулярной линии AB на звене, т.е. 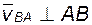 . Кроме того, скорость
. Кроме того, скорость 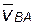 связана с величиной и направлением угловой скорости этого звена
связана с величиной и направлением угловой скорости этого звена
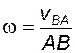 ; (2.2)
; (2.2)
здесь нужно учитывать, что относительная скорость 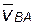 направлена на ту букву плана, которая в обозначении вектора стоит первой (в данном случае – по линии ab на букву b плана).
направлена на ту букву плана, которая в обозначении вектора стоит первой (в данном случае – по линии ab на букву b плана).
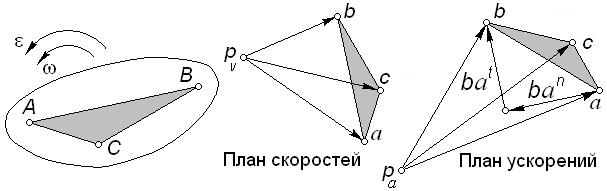
Рис. 2.1
Если скорости двух точек A и B звена известны, то для нахождения скорости любой третьей точки C этого же звена можно воспользоваться соотношением подобия:  ˆ
ˆ  .
.
Соотношение для ускорений точек A и B получим, продифференцировав (2.1):
 ; (2.3)
; (2.3)
нормальное относительное ускорение 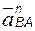 всегда направлено вдоль вектора
всегда направлено вдоль вектора 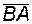 и его величина
и его величина
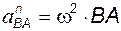 . (2.4)
. (2.4)
Вектор  (или
(или  ); его величина и направление устанавливаются по результату построения плана ускорений (рис. 2.1); тогда угловое ускорение звена
); его величина и направление устанавливаются по результату построения плана ускорений (рис. 2.1); тогда угловое ускорение звена
 . (2.5)
. (2.5)
Если ускорения точек A и B были найдены, то для любой третьей точки C можно воспользоваться соотношением подобия по аналогии с тем, которое применили при построении плана скоростей:  ˆ
ˆ  .
.
· Два звена, участвующих в плоскопараллельном движении, образуют поступательную пару.
Абсолютное движение звена 3 (рис. 2.2) относительно неподвижной плоскости может быть каким угодно (в частности, звено может быть неподвижным, или неподвижной может быть только точка B этого звена и т.д.). Но в любом случае это движение можно считать сложным, получающимся в результате сложения двух движений: плоскопараллельного движения направляющей 2 (переносного) и прямолинейного поступательного движения звена 3 по направляющей (относительного).
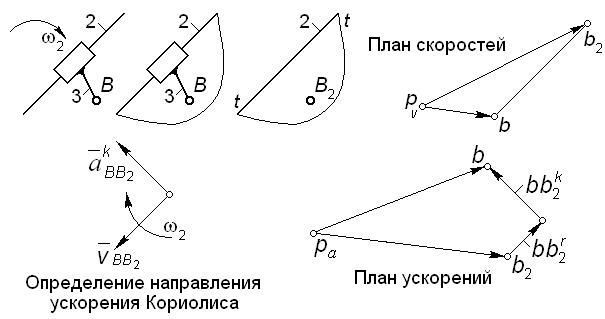
|
| Рис. 2.2
|
Для скорости точки B звена 3 отмеченный факт отражают в такой записи:
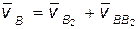 ; (2.6)
; (2.6)
здесь 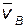 – абсолютная скорость точки B звена 3;
– абсолютная скорость точки B звена 3;
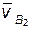 – скорость точки B в переносном движении в данный момент времени (по определению – это абсолютная скорость той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B);
– скорость точки B в переносном движении в данный момент времени (по определению – это абсолютная скорость той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B);
 – скорость перемещения звена 3 по направляющей 2.
– скорость перемещения звена 3 по направляющей 2.
Важно отметить, что абсолютные скорости точек B и B2 могут быть любыми, но концы векторов 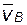 и
и  на плане скоростей (рис. 2.2) всегда будут находиться на одной прямой, параллельной направляющей 2, т.е.
на плане скоростей (рис. 2.2) всегда будут находиться на одной прямой, параллельной направляющей 2, т.е. 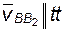 , или
, или 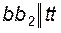 (скорость
(скорость 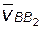 на плане направлена по прямой
на плане направлена по прямой 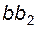 в сторону точки b).
в сторону точки b).
Чтобы получить требуемое соотношение для ускорений точек B и B2, продифференцируем (2.6); учитывая, что
 ;
; 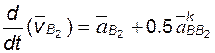 ;
; 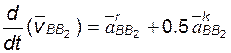 ,
,
получим
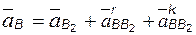 ; (2.7)
; (2.7)
в этом уравнении:
 – абсолютное ускорение точки B звена 3;
– абсолютное ускорение точки B звена 3;
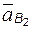 – ускорение точки B в переносном движении в данный момент времени (абсолютное ускорение той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B);
– ускорение точки B в переносном движении в данный момент времени (абсолютное ускорение той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B);
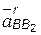 – ускорение в движении звена 3 по направляющей 2 (если направляющая 2 прямолинейна, как в нашем случае, то
– ускорение в движении звена 3 по направляющей 2 (если направляющая 2 прямолинейна, как в нашем случае, то 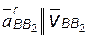 , или
, или 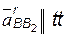 );
);
 – ускорение Кориолиса (поворотное ускорение), возникает при перемещении точки по звену, движущемуся непоступательно; для нашего случая
– ускорение Кориолиса (поворотное ускорение), возникает при перемещении точки по звену, движущемуся непоступательно; для нашего случая
 ; (2.8)
; (2.8)
направление ускорения 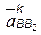 совпадает с направлением вектора
совпадает с направлением вектора 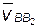 , повернутого на 90° в сторону переносной угловой скорости
, повернутого на 90° в сторону переносной угловой скорости 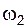 (отметим, что при соединении звеньев с помощью поступательной пары их угловые скорости и ускорения одинаковы, т.е.
(отметим, что при соединении звеньев с помощью поступательной пары их угловые скорости и ускорения одинаковы, т.е. 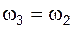 ,
,  ).
).
Заметим, что рассмотренных двух типов кинематических соотношений достаточно для исследования кинематики любой плоской структурной группы.
Таблица 2.1
Определение скоростей и ускорений для структурных групп второго класса
| Вид
группы
| Схема структурной группы
| Требуется определить
| Уравнения для определения линейных и угловых скоростей
| Уравнения для определения линейных и угловых ускорений
|
|
|
|
|
|
|
|
1-й вид
|  Известны: положения точек A и C;
скорости
Известны: положения точек A и C;
скорости 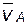 и и  ;
ускорения ;
ускорения  и и 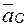 . .
| положение
точки B;
 ; ;
 ; ;
 . .
|  ; ;
 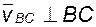 ; ;
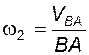 ; ;  . .
| 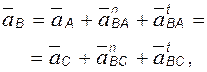
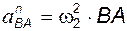 ; ; 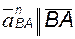 ; ;
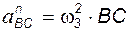 ; ; 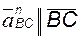 ; ;
 ; ;  ; ;
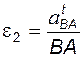 ; ; 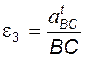 . .
|
 2-й вид 2-й вид
| 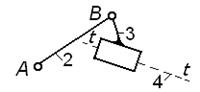 Известны: положение точки A и звена 4;
скорость
Известны: положение точки A и звена 4;
скорость  , угловая скорость , угловая скорость  , скорость любой точки звена 4;
ускорение , скорость любой точки звена 4;
ускорение  , угловое ускорение , угловое ускорение  , ускорение любой точки звена 4. , ускорение любой точки звена 4.
| положение
точки B;
 ; ;
 ; ;
 ;
параметры относительного движения звеньев 3 и 4. ;
параметры относительного движения звеньев 3 и 4.
| 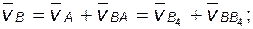
 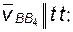
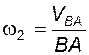 ; ;
 ; ;
| 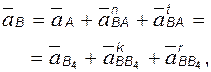
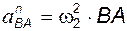 ; ; 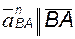 ; ;
 ; ;
 ; ;
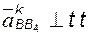 ; ; 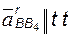 ; ;
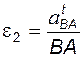 ; ;  . .
|
 Продолжение табл. 2.1
Продолжение табл. 2.1
|
|
|
|
|
|
|
3-й вид
|  Известны: положения точек A и B;
скорости
Известны: положения точек A и B;
скорости 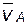 и и 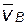 ;
ускорения ;
ускорения  и и  . .
| положения звеньев
2 и 3;
параметры относительного движения звеньев 2 и 3;
 ; ;
 . .
| 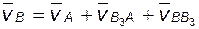 ; ;
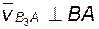 ; ;  ; ;
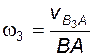 ; ; 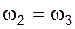 . .
| 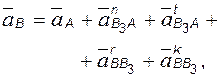
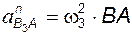 ; ;  ; ;
 ; ;
 ; ;
 ; ;  ; ;
 ; ; 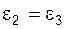 . .
|
|
4-й вид
| 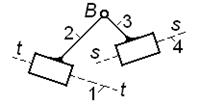 Известны: положения звеньев 1 и 4; угловые скорости
Известны: положения звеньев 1 и 4; угловые скорости 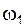 и и  ; угловые ускорения ; угловые ускорения 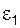 и и  ; скорости и ускорения любых точек звеньев 1 и 4. ; скорости и ускорения любых точек звеньев 1 и 4.
| положение
точки B;
 ; ;
 ; ;
 ; параметры относительного движения звеньев в поступательных парах. ; параметры относительного движения звеньев в поступательных парах.
| 
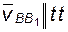 ; ;  ; ;
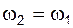 ; ;  ; ;
| 
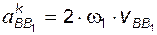 ; ;
 ; ;  ; ;
 ; ;
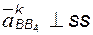 ; ;  ; ;
 ; ;  . .
|
Окончание табл. 2.1
|
|
|
|
|
|
|
5-й вид
| 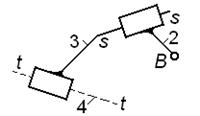 Известны: положения точки B и звена 4; скорость Известны: положения точки B и звена 4; скорость 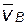 ; угловая скорость ; угловая скорость  ; ускорение ; ускорение  ; угловое ускорение ; угловое ускорение  ; скорость и ускорение любой точки звена 4. ; скорость и ускорение любой точки звена 4.
| положения звеньев
2 и 3;
параметры относительного движения звеньев в поступательных парах;
 ; ;

| 
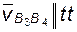 ; ;  ; ;
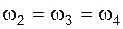 . .
| 
 ; ;
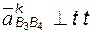 ; ;  ; ;
 ; ;
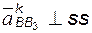 ; ; 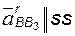 ; ;
 . .
|
Вопросы для самопроверки
1. Опишите последовательность кинематического анализа плоского механизма.
2. Запишите уравнения планов скоростей и ускорений для любой структурной группы II класса, содержащей внутреннюю поступательную пару.
3. Запишите уравнения планов скоростей и ускорений для любой структурной группы II класса, содержащей хотя бы одну внешнюю поступательную пару.
4. Как определяют величину и направление ускорения Кориолиса?
5. В каких случаях при построении планов скоростей и ускорений применяют метод подобия?
6. По какому признаку можно установить, является ли равномерным (или неравномерным) относительное движение звеньев, образующих поступательную пару?
Задача 2.05
Для структурной группы имеется уравнение плана ускорений
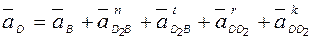 .
Написать для этой группы:
1) уравнение плана скоростей; формулы для расчета угловой скорости .
Написать для этой группы:
1) уравнение плана скоростей; формулы для расчета угловой скорости 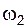 и углового ускорения и углового ускорения  ;
2) формулы для расчета нормального и кориолисова ускорений. ;
2) формулы для расчета нормального и кориолисова ускорений.
| |
| | |
Задача 2.06
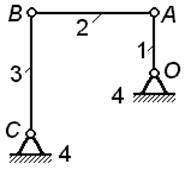
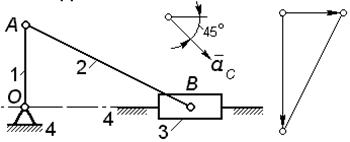
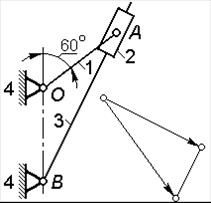
| В рассматриваемом положении механизма звенья 1 и 3 вертикальны, звено 2 горизонтально.
Звено 1 вращается равномерно с угловой скоростью  =10 рад / с.
Длины звеньев: AB = BC = 2× OA.
Найти величину и направление углового ускорения звена 2. =10 рад / с.
Длины звеньев: AB = BC = 2× OA.
Найти величину и направление углового ускорения звена 2.
|
| |
|
Задача 2.07
В рассматриваемом положении механизма звенья 1 и 3 вертикальны, звено 2 горизонтально.
Звено 1 вращается равномерно с угловой скоростью  =10 рад / с.
Длины звеньев: AB = BC = 2× OA.
Найти величину и направление углового ускорения звена 2. =10 рад / с.
Длины звеньев: AB = BC = 2× OA.
Найти величину и направление углового ускорения звена 2.
| 
|
| |
|
Задача 2.08

| Определить скорость и ускорение точки B звена 2; указать направления обоих векторов для заданного положения механизма.
Исходные данные:  ; ;  ; ; 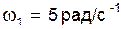 ; кривошип ; кривошип 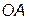 в текущем положении вертикален. в текущем положении вертикален.
|
| | | | | |
Задача 2.09
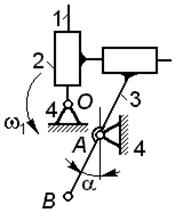
| Для механизма крестово-кулисной муфты определить скорость и ускорение точки B звена 3; указать направления обоих векторов.
В текущем положении механизма зве- но 1 вертикально и вращается равномерно с угловой скоростью ω1 = 10 рад/с, звено 3 отклонено от вертикали на угол 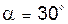 . Размер АВ = 0.3 м. . Размер АВ = 0.3 м.
|
Задача 2.10
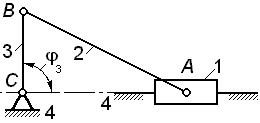
|
В текущем положении механизма угол 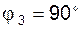 ползун 1 движется равномерно.
Размеры звеньев: длина кривошипа ползун 1 движется равномерно.
Размеры звеньев: длина кривошипа  , длина шатуна , длина шатуна  .
Определить точное соотношение угловых ускорений звеньев .
Определить точное соотношение угловых ускорений звеньев  в указанном положении. в указанном положении.
|
Задача 2.11(см. рисунок к задаче 2.10)
Установить величину отношения угловых ускорений звеньев 2 и 3 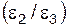 при равномерном движении ползуна 1 в изображенном положении кривошипно-ползунного механизма (т.е. при угле при равномерном движении ползуна 1 в изображенном положении кривошипно-ползунного механизма (т.е. при угле 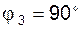 ). Соотношение длин звеньев: ). Соотношение длин звеньев:  . .
|
Задача 2.12(см. рисунок к задаче 2.10)
Доказать, что при равномерном движении ползуна 1 в изображенном положении механизма (т.е. при угле 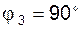 ) угловые ускорения звеньев 2 и 3 одинаковы по величине и направлению. ) угловые ускорения звеньев 2 и 3 одинаковы по величине и направлению.
|
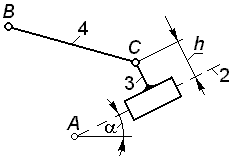
Задача 2.13 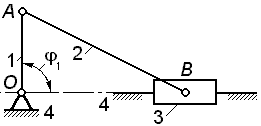 Кривошип 1 вращается с угловым ускорением Кривошип 1 вращается с угловым ускорением 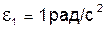 ; при каком значе-нии его угловой скорости ; при каком значе-нии его угловой скорости 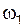 ползун 3 в рассматриваемом положении механизма (т.е. при угле ползун 3 в рассматриваемом положении механизма (т.е. при угле  ) будет двигаться равномерно?
Соотношение длин звеньев: ) будет двигаться равномерно?
Соотношение длин звеньев: 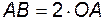 . .
|
| | | |
 Задача 2.14
Задача 2.14
Для кинематической цепи известны: размеры звеньев BC и h; положение, скорость  и ускорение
и ускорение 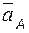 точки A; положение (угол a), угловая скорость
точки A; положение (угол a), угловая скорость 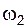 и угловое ускорение
и угловое ускорение 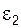 звена 2; положение, скорость
звена 2; положение, скорость  и ускорение
и ускорение 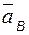 точки B.
точки B.
Описать порядок построения положения точки С; написать уравнения планов скоростей и ускорений, в результате решения которых будут найдены скорость и ускорение точки С, а также угловая скорость и угловое ускорение звеньев 3 и 4.
Задача 2.15
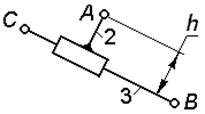
| Для кинематической цепи известны: размеры звеньев BC и h; положение, скорость 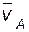 и ускорение и ускорение 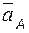 точки A; положение, скорость точки A; положение, скорость  и ускорение и ускорение  точки B.
Написать совокупность векторных уравнений и скалярных зависимостей для определения скорости и ускорения точки С. точки B.
Написать совокупность векторных уравнений и скалярных зависимостей для определения скорости и ускорения точки С.
|
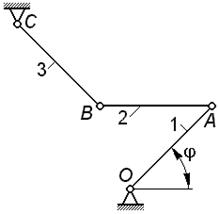
Задача 2.16
Взаимное расположение шарниров O и C таково, что при 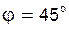 звено AB горизонтально и OA звено AB горизонтально и OA 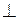 CB. Установить соотношения угловых скоростей звеньев ( CB. Установить соотношения угловых скоростей звеньев (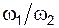 ) и ( ) и (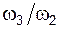 ) для указанного положения механизма.
Размеры звеньев: OA=AB=CB. ) для указанного положения механизма.
Размеры звеньев: OA=AB=CB.
| 
|
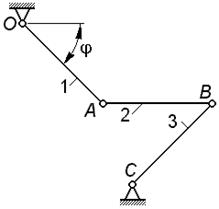
Задача 2.17
Размеры звеньев механизма: OA=AB=CB; взаимное расположение шарниров O и C таково, что при  звено AB горизонтально и OA звено AB горизонтально и OA 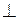 CB.
Установить соотношения угловых скоростей звеньев ( CB.
Установить соотношения угловых скоростей звеньев (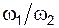 ) и ( ) и (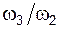 ) для указанного положения механизма. ) для указанного положения механизма.
| 
|
| | | |
Задача 2.18

| Написать все уравнения, необходимые для нахождения скорости и ускорения точки C звена 2 методом планов; при написании векторных уравнений указать, в какой мере известны те или иные векторы, входящие в него.
Геометрические параметры звеньев считать заданными, а положения, скорости и ускорения точек A и B – известными для текущего момента времени.
|
Задача 2.19
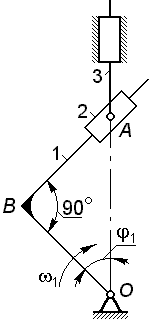
Для секансного механизма определить скорость точки A в положении, определяемом углом 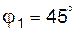 .
Размер .
Размер  ; входное звено вращается с угловой скоростью ; входное звено вращается с угловой скоростью  . .
| 
|
Задача 2.20(см. рисунок к задаче 2.19)
Для секансного механизма определить скорость скольжения в поступательной паре (1-2) в положении, определяемом углом 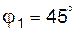 .
Размер .
Размер  ; входное звено вращается с угловой скоростью ; входное звено вращается с угловой скоростью  . .
|
Задача 2.21
Для синусного механизма определить аналитически скорость и ускорение точки B в положении, определяемом углом 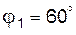 .
Размеры .
Размеры  , , 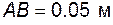 ; входное звено вращается с угловой скоростью ; входное звено вращается с угловой скоростью  . .
| 
|
| | | | |
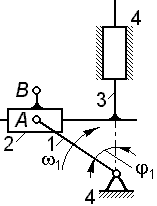
| Задача 2.22
Для синусного механизма определить аналитически скорость и ускорение в относительном движении ползуна 2 по звену 3 в положении, определяемом углом 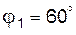 .
Размер .
Размер  ; входное звено вращается с угловой скоростью ; входное звено вращается с угловой скоростью  . .
|
Задача 2.23
Для тангенсного механизма найти аналитически скорость точки A в положении, определяемом углом 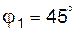 .
Размер .
Размер  ; кулиса 1 вращается с угловой скоростью ; кулиса 1 вращается с угловой скоростью  . .
| 
|
Задача 2.24(см. рисунок к задаче 2.23)
Для тангенсного механизма найти аналитически скорость скольжения в поступательной паре (1-2) в положении, определяемом углом 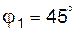 .
Размер .
Размер 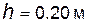 ; кулиса 1 вращается с постоянной угловой скоростью ; кулиса 1 вращается с постоянной угловой скоростью  . .
|
Задача 2.25
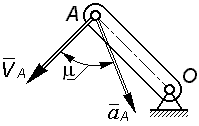
| Рычаг длиной OA =0.5 м вращается ускоренно; скорость его конца  = 2 м/с, вектор ускорения = 2 м/с, вектор ускорения 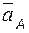 направлен под углом направлен под углом 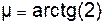 к вектору скорости.
Определить угловое ускорение e рычага. к вектору скорости.
Определить угловое ускорение e рычага.
|
Задача 2.26(см. рисунок к задаче 2.25)
Рычаг длиной OA =0.5 м вращается ускоренно; скорость его конца  = 2 м/с, вектор ускорения = 2 м/с, вектор ускорения 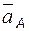 направлен под углом направлен под углом  к вектору скорости.
Определить величину ускорения к вектору скорости.
Определить величину ускорения 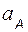 . .
|
| | | | |

 . (2.1)
. (2.1) –
–  полюс плана, в который помещают начала векторов абсолютных скоростей всех интересующих нас точек. Скорости
полюс плана, в который помещают начала векторов абсолютных скоростей всех интересующих нас точек. Скорости 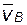 и
и 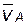 могут быть любыми, но концы этих векторов на плане обязательно находятся на одной прямой, перпендикулярной линии AB на звене, т.е.
могут быть любыми, но концы этих векторов на плане обязательно находятся на одной прямой, перпендикулярной линии AB на звене, т.е. 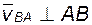 . Кроме того, скорость
. Кроме того, скорость 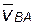 связана с величиной и направлением угловой скорости этого звена
связана с величиной и направлением угловой скорости этого звена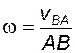 ; (2.2)
; (2.2)
 ˆ
ˆ  .
. ; (2.3)
; (2.3)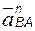 всегда направлено вдоль вектора
всегда направлено вдоль вектора 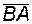 и его величина
и его величина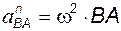 . (2.4)
. (2.4) (или
(или 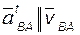 ); его величина и направление устанавливаются по результату построения плана ускорений (рис. 2.1); тогда угловое ускорение звена
); его величина и направление устанавливаются по результату построения плана ускорений (рис. 2.1); тогда угловое ускорение звена . (2.5)
. (2.5)
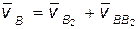 ; (2.6)
; (2.6)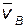 – абсолютная скорость точки B звена 3;
– абсолютная скорость точки B звена 3;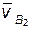 – скорость точки B в переносном движении в данный момент времени (по определению – это абсолютная скорость той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B);
– скорость точки B в переносном движении в данный момент времени (по определению – это абсолютная скорость той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B); – скорость перемещения звена 3 по направляющей 2.
– скорость перемещения звена 3 по направляющей 2. на плане скоростей (рис. 2.2) всегда будут находиться на одной прямой, параллельной направляющей 2, т.е.
на плане скоростей (рис. 2.2) всегда будут находиться на одной прямой, параллельной направляющей 2, т.е. 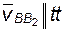 , или
, или 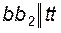 (скорость
(скорость 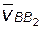 на плане направлена по прямой
на плане направлена по прямой 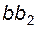 в сторону точки b).
в сторону точки b). ;
; 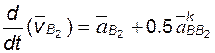 ;
; 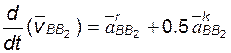 ,
,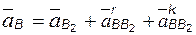 ; (2.7)
; (2.7) – абсолютное ускорение точки B звена 3;
– абсолютное ускорение точки B звена 3;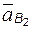 – ускорение точки B в переносном движении в данный момент времени (абсолютное ускорение той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B);
– ускорение точки B в переносном движении в данный момент времени (абсолютное ускорение той точки B2 направляющей 2, с которой в данный момент времени совпадает движущаяся точка B);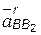 – ускорение в движении звена 3 по направляющей 2 (если направляющая 2 прямолинейна, как в нашем случае, то
– ускорение в движении звена 3 по направляющей 2 (если направляющая 2 прямолинейна, как в нашем случае, то 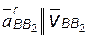 , или
, или 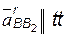 );
); – ускорение Кориолиса (поворотное ускорение), возникает при перемещении точки по звену, движущемуся непоступательно; для нашего случая
– ускорение Кориолиса (поворотное ускорение), возникает при перемещении точки по звену, движущемуся непоступательно; для нашего случая ; (2.8)
; (2.8)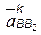 совпадает с направлением вектора
совпадает с направлением вектора 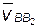 , повернутого на 90° в сторону переносной угловой скорости
, повернутого на 90° в сторону переносной угловой скорости 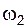 (отметим, что при соединении звеньев с помощью поступательной пары их угловые скорости и ускорения одинаковы, т.е.
(отметим, что при соединении звеньев с помощью поступательной пары их угловые скорости и ускорения одинаковы, т.е. 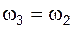 ,
,  ).
). Известны: положения точек A и C;
скорости
Известны: положения точек A и C;
скорости 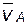 и
и  ;
ускорения
;
ускорения  и
и 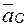 .
.
 ;
;
 ;
;
 .
.
 ;
;

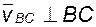 ;
;
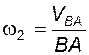 ;
;  .
.
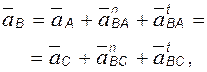
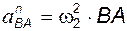 ;
; 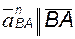 ;
;
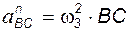 ;
; 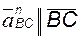 ;
;
 ;
;  ;
;
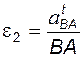 ;
; 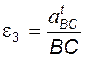 .
.
 2-й вид
2-й вид
 Известны: положение точки A и звена 4;
скорость
Известны: положение точки A и звена 4;
скорость  , скорость любой точки звена 4;
ускорение
, скорость любой точки звена 4;
ускорение  , ускорение любой точки звена 4.
, ускорение любой точки звена 4.
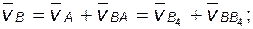
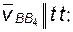
 ;
;
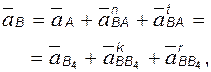
 ;
;
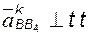 ;
; 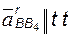 ;
;
 .
.
 Продолжение табл. 2.1
Продолжение табл. 2.1 Известны: положения точек A и B;
скорости
Известны: положения точек A и B;
скорости 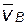 ;
ускорения
;
ускорения 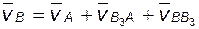 ;
;
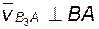 ;
;  ;
;
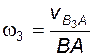 ;
; 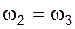 .
.
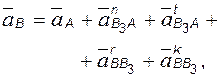
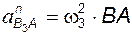 ;
;  ;
;
 ;
;
 ;
;
 ;
;  ;
;
 ;
; 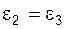 .
.
 Известны: положения звеньев 1 и 4; угловые скорости
Известны: положения звеньев 1 и 4; угловые скорости 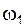 и
и 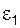 и
и 
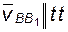 ;
;  ;
;
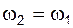 ;
; 
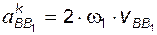 ;
;
 ;
;  ;
;
 ;
;
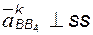 ;
;  ;
;
 ;
;  Известны: положения точки B и звена 4; скорость
Известны: положения точки B и звена 4; скорость 
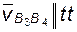 ;
;  ;
;
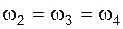 .
.

 ;
;
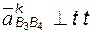 ;
;  ;
;
 ;
;
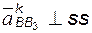 ;
; 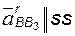 ;
;
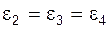 .
.
 .
Написать для этой группы:
1) уравнение плана ускорений;
2) формулы для вычисления угловой скорости и углового ускорения звена 3.
.
Написать для этой группы:
1) уравнение плана ускорений;
2) формулы для вычисления угловой скорости и углового ускорения звена 3.
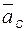 ускорения точки C.
ускорения точки C.

 ), если OA = OB.
), если OA = OB.
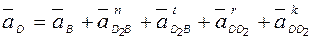 .
Написать для этой группы:
1) уравнение плана скоростей; формулы для расчета угловой скорости
.
Написать для этой группы:
1) уравнение плана скоростей; формулы для расчета угловой скорости  ;
2) формулы для расчета нормального и кориолисова ускорений.
;
2) формулы для расчета нормального и кориолисова ускорений.

 =10 рад / с.
Длины звеньев: AB = BC = 2× OA.
Найти величину и направление углового ускорения звена 2.
=10 рад / с.
Длины звеньев: AB = BC = 2× OA.
Найти величину и направление углового ускорения звена 2.


 ;
;  ;
; 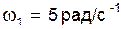 ; кривошип
; кривошип 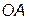 в текущем положении вертикален.
в текущем положении вертикален.

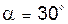 . Размер АВ = 0.3 м.
. Размер АВ = 0.3 м.

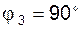 ползун 1 движется равномерно.
Размеры звеньев: длина кривошипа
ползун 1 движется равномерно.
Размеры звеньев: длина кривошипа  , длина шатуна
, длина шатуна  .
Определить точное соотношение угловых ускорений звеньев
.
Определить точное соотношение угловых ускорений звеньев  в указанном положении.
в указанном положении.
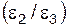 при равномерном движении ползуна 1 в изображенном положении кривошипно-ползунного механизма (т.е. при угле
при равномерном движении ползуна 1 в изображенном положении кривошипно-ползунного механизма (т.е. при угле  .
.
 Кривошип 1 вращается с угловым ускорением
Кривошип 1 вращается с угловым ускорением 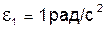 ; при каком значе-нии его угловой скорости
; при каком значе-нии его угловой скорости 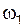 ползун 3 в рассматриваемом положении механизма (т.е. при угле
ползун 3 в рассматриваемом положении механизма (т.е. при угле  ) будет двигаться равномерно?
Соотношение длин звеньев:
) будет двигаться равномерно?
Соотношение длин звеньев: 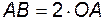 .
.
 Задача 2.14
Задача 2.14 и ускорение
и ускорение 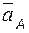 точки A; положение (угол a), угловая скорость
точки A; положение (угол a), угловая скорость 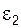 звена 2; положение, скорость
звена 2; положение, скорость  и ускорение
и ускорение 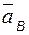 точки B.
точки B.
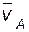 и ускорение
и ускорение  и ускорение
и ускорение  точки B.
Написать совокупность векторных уравнений и скалярных зависимостей для определения скорости и ускорения точки С.
точки B.
Написать совокупность векторных уравнений и скалярных зависимостей для определения скорости и ускорения точки С.
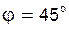 звено AB горизонтально и OA
звено AB горизонтально и OA 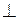 CB. Установить соотношения угловых скоростей звеньев (
CB. Установить соотношения угловых скоростей звеньев (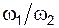 ) и (
) и (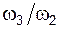 ) для указанного положения механизма.
Размеры звеньев: OA=AB=CB.
) для указанного положения механизма.
Размеры звеньев: OA=AB=CB.

 звено AB горизонтально и OA
звено AB горизонтально и OA 

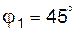 .
Размер
.
Размер  ; входное звено вращается с угловой скоростью
; входное звено вращается с угловой скоростью  .
.

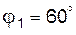 .
Размеры
.
Размеры  ,
, 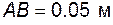 ; входное звено вращается с угловой скоростью
; входное звено вращается с угловой скоростью 

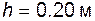 ; кулиса 1 вращается с угловой скоростью
; кулиса 1 вращается с угловой скоростью 
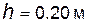 ; кулиса 1 вращается с постоянной угловой скоростью
; кулиса 1 вращается с постоянной угловой скоростью 
 = 2 м/с, вектор ускорения
= 2 м/с, вектор ускорения 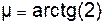 к вектору скорости.
Определить угловое ускорение e рычага.
к вектору скорости.
Определить угловое ускорение e рычага.
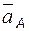 направлен под углом
направлен под углом  к вектору скорости.
Определить величину ускорения
к вектору скорости.
Определить величину ускорения 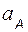 .
.



