Кинематика замкнутых механизмов
Проанализируем структуру комбинированного механизма, представленного на рис. 3.11; он включает в себя: дифференциальную ступень ( Кинематика дифференциальной ступени описывается формулой Р. Виллиса
если бы любые две из трех угловых скоростей
Таким образом, звенья Если учесть соотношения
тогда передаточное отношение механизма
Таким образом, для анализа кинематики подобных механизмов можно придерживаться следующей методики: 1) выделить в схеме дифференциальную ступень, содержащую водило, размещенные на нем сателлиты и центральные колеса, зацепляющиеся с этими сателлитами; для выделенной ступени написать формулу Р. Виллиса по типу (3.23), ни одна из угловых скоростей не должна быть равна нулю (т.е. ступень не должна содержать неподвижных колес); 2) выделить в схеме замыкающую кинематическую цепь, связывающую между собой какие-то центральные звенья дифференциальной ступени; если эта цепь рядовая, то написать для нее формулу по типу (3.24); 3) написать уравнения внутренних кинематических связей (для данного механизма – формулы 4) написать уравнения внешних кинематических связей (для данного механизма – формулы 5) используя зависимости, полученные в пунктах 2 – 4, выразить каждую угловую скорость, входящую в формулу Р. Виллиса (п. 1) через
|


 ) и рядовую кинематическую цепь (
) и рядовую кинематическую цепь (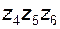 ).
).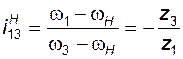 ; (3.23)
; (3.23)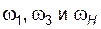 у этой ступени могли быть независимыми, то данный механизм имел бы две степени свободы. Однако, поскольку
у этой ступени могли быть независимыми, то данный механизм имел бы две степени свободы. Однако, поскольку 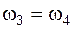 и
и  , то угловые скорости
, то угловые скорости 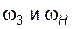 дифференциала связаны между собой соотношением
дифференциала связаны между собой соотношением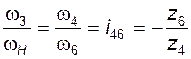 . (3.24)
. (3.24) и H дифференциала имеют жесткую кинематическую связь в виде рядовой цепи (
и H дифференциала имеют жесткую кинематическую связь в виде рядовой цепи (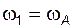 и
и 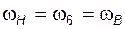 , то (3.23) можно записать в виде
, то (3.23) можно записать в виде ; (3.25)
; (3.25) . (3.26)
. (3.26)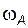 или
или  , чтобы получить уравнение по типу (3.25); из этого уравнения вывести формулу для
, чтобы получить уравнение по типу (3.25); из этого уравнения вывести формулу для  .
.


