Тестовое задание 6 страница
E) треугольной матрицей
211. Нормировать элемент А) В) С) D) E)
212. Нормировать элемент А) В) С) D) E)
213. Какие из указанных элементов А) В) С) D) E)
214. Укажите разложение элемента А) В) С) D) E)
215. Какие из указанных элементов А) В) С) D) E)
216. Укажите разложение элемента А) В) С) D) E)
217. Составьте матрицу Грамма для базиса А) В) С) D) E)
218. Составьте матрицу Грамма для базиса А) В) С) D) E)
219. Составьте матрицу Грамма для базиса А) В) С) D) E)
220. Составьте матрицу Грамма для базиса А) В) С) D) E)
221. Уравнение прямой с угловым коэффициентом: имеет вид А) В) С) D) Е)
222. Укажите условие перпендикулярности прямых, заданных уравнениями с угловым коэффициентом: А) В) С) D) Е)
223. Укажите условие параллельности прямых, заданных общими уравнениями A) B) C) D) E)
224. Укажите формулу, определяющую угол A) B) C) D) E)
225. Укажите уравнение прямой в отрезках: A) B) C) D) E)
226. Укажите формулу, определяющую угол А) B) C) D) E)
227. Укажите уравнение прямой, проходящей через данную точку A) B) C) D) E)
228. Прямая, проходит через данные точки A) B) C) D) E)
229. Укажите координаты направляющего вектора A) B) C) D) E)
230. Укажите параметрические уравнения прямой, заданной на плоскости А) B) C) D) E)
231. Написать уравнение прямой с угловым коэффициентом, проходящей через две точки A) B) C) D) E)
232. Найти угловой коэффициент прямой A) B) C) D) E)
233. Даны две точки на отрезке A) B) C) D) E)
234. Даны точки A) B) C) D) E)
235. Составьте уравнение прямой, проходящей через точку A) B) C) D) E)
236. Написать общее уравнение перпендикулярной линии проходящей через середину A) B) C) D) E)
237. Определить значение А) В) С) D) Е)
238. Найти расстояние от точки А) В) С) D) -3 Е) 5
239. Определить координаты нормального вектора А) В) С) D) Е)
240. Найти точку пересечения прямых А) В) С) D) Е)
241..Каноническое уравнение эллипса имеет вид: А) В) С) D) Е)
242. Укажите координаты вершин А) В) С) D) Е)
243. Каноническое уравнение гиперболы имеет вид: А) В) С) D) Е)
244. Уравнение асимптот гиперболы имеет вид: А) В) С) D) Е)
245. Эксцентриситет А) В) С) D) Е)
246. Уравнение директрисы параболы А) В) С) D) Е)
247. Укажите координаты фокуса параболы А) В) С) D) Е)
248. Если А) уравнение окружности В) уравнение эллипса С) уравнение гиперболы D) уравнение параболы Е) уравнение лемнискаты Бернулли
249. Если ось симметрии параболы – ось ординат, то уравнение параболы имеет вид: А) В) С) D) Е)
250. Если ось симметрии параболы – ось абсцисс, то уравнение параболы имеет вид: А) В) С) D) Е)
251. Определить координаты центра окружности
|

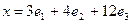 , если базис
, если базис 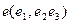 является ортонормированным.
является ортонормированным.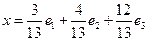
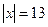
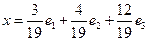
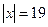
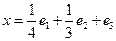
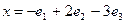 , если базис
, если базис 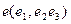 является ортонормированным.
является ортонормированным.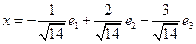

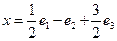
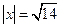
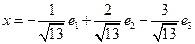
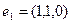 ,
, 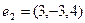 ,
, 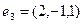 являются ортогональными элементами?
являются ортогональными элементами?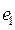 и
и 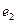
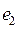 и
и 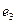
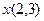 по ортогональному базису
по ортогональному базису 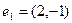 ,
, 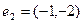 .
.
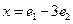
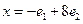
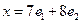
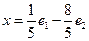
 ,
,  ,
,  являются ортогональными элементами?
являются ортогональными элементами?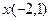 по ортогональному базису
по ортогональному базису 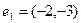 ,
, 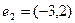 .
.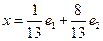
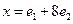
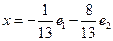
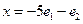
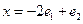
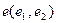 , заданного в пространстве
, заданного в пространстве 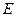 , где
, где 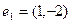 ,
, 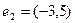 .
.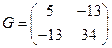

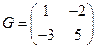

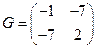
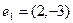 ,
, 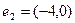 .
.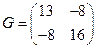
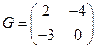
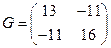
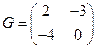
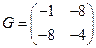
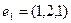 ,
, 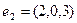 ,
, 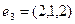 .
.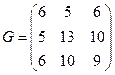


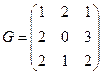
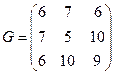
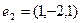 ,
, 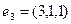 .
.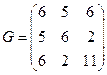

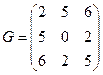

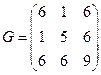



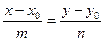
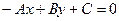


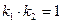
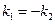
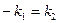
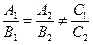
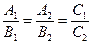
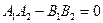
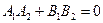

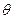 между двумя прямыми
между двумя прямыми 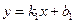 и
и 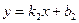 :
:
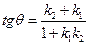
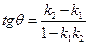
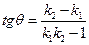
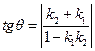
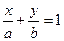


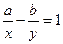
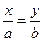
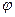 между двумя прямыми, заданными общими уравнениями:
между двумя прямыми, заданными общими уравнениями: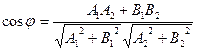


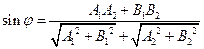

 в данном направлении.
в данном направлении.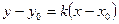
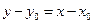

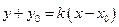
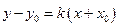
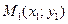 ,
, 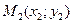 .Укажите формулы координат точки
.Укажите формулы координат точки  , лежащей на этой прямой и делящей отрезок
, лежащей на этой прямой и делящей отрезок 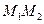 в отношении
в отношении 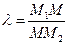 :
: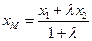 ,
, 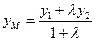
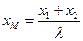 ,
, 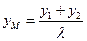
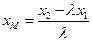 ,
, 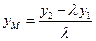
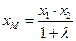 .
. 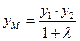
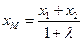 ,
, 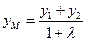
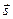 прямой, если координаты нормального вектора прямой
прямой, если координаты нормального вектора прямой 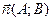 ,
,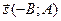
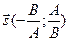
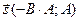

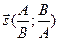
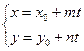
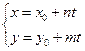
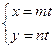

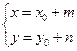
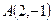 и
и  :
: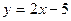
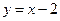

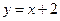
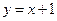
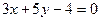 :
: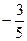

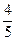
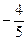
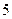
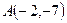 и
и 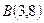 . Найдите на этом отрезке точку делящую его в отношении
. Найдите на этом отрезке точку делящую его в отношении 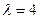 :
: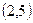
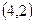
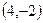
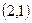
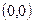
 и
и 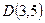 . Найдите координаты середины отрезка
. Найдите координаты середины отрезка 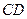 :
: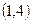
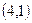
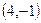

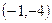
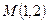 параллельно прямой
параллельно прямой  :
: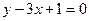

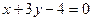
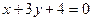
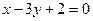
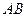 , если
, если 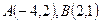 :
: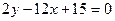
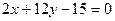
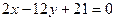
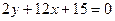

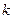 , при котором прямые
, при котором прямые 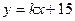 и
и 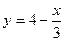 будут параллельны:
будут параллельны: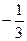
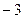
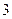
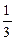
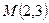 до прямой
до прямой 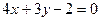 :
: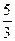
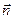 прямой
прямой  :
: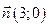

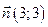
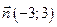
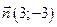
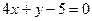 и
и 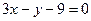 :
:
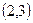
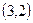
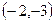
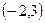
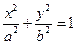
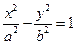
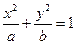
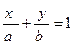
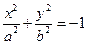
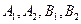 эллипса:
эллипса: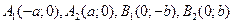
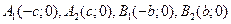

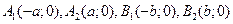
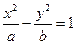
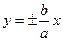
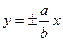
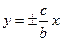
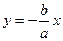
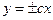
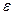 эллипса, гиперболы вычисляется по формуле:
эллипса, гиперболы вычисляется по формуле: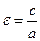
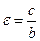
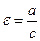
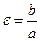

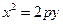 имеет вид:
имеет вид: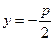
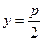

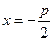

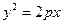 :
:
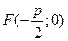
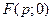
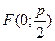
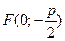
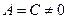 и
и  в уравнении
в уравнении 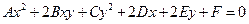 , то данное уравнение есть
, то данное уравнение есть
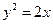
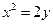
 :
:


