Тестовое задание 5 страница
177. Линейный оператор А) В) С) D) Е)
178. Линейный оператор А) В) С) D) Е)
179. Как называется ненулевой вектор А) собственным вектором оператора В) независимым вектором оператора С) вектором оператора D) базисным вектором линейного пространства Е) линейно-независимым вектором оператора
180. Как называется множество собственных значений линейного оператора? А) спектром линейного оператора В) дефектом линейного оператора С) рангом линейного оператора D) областью значений оператора. Е) ядром линейного оператора
181. Укажите характеристическое уравнение оператора А) В) С) D) Е)
182. Укажите матрицу линейного оператора А) матрица В) матрица С) матрица D) матрица Е) матрица
183. Укажите необходимое и достаточное условие того, чтобы число А) В) С) D) Е)
184. Укажите необходимое и достаточное условие того чтобы матрица А) элементы базиса должны быть собственными векторами оператора В) элементы базиса должны быть ортогональными векторами С) элементы базиса должны быть единичными векторами D) элементы базиса составляют ортонормированный базис Е) элементы базиса должны быть независимыми векторами оператора
185. Для оператора А) В) С) D) Е)
186. Укажите характеристическое уравнение оператора А) В) С) D) Е)
187. Линейный оператор А) В) С) D) Е)
188. Линейный оператор А) В) С) D) Е)
189. Составьте характеристический многочлен матрицы А) В) С) D) Е)
190. Укажите характеристическое уравнение оператора А) В) С) D) Е)
191. Укажите характеристическое уравнение оператора А) В) С) D) Е)
192. Найти собственные значения оператора А) В) нет собственных значений С) D) Е)
193. Найти собственные значения оператора А) В) С) D) Е)
194. Составить систему уравнений для определения собственного вектора, соответствующего собственному значению А) В) С) D) Е)
195 Составить систему уравнений для определения собственного вектора, соответствующего собственному значению А) В) С) D) Е)
196. Найти собственный вектор, соответствующий собственному значению А) В) С) D) Е)
197. Найти собственный вектор, соответствующий собственному значению А) В) С) D) Е)
198. Найти собственные значения оператора А) В) С) D) Е)
199. Найти собственные значения оператора А) В) С) D) Е)
200. Найти собственные значения оператора А) В) С) D) Е)
201. Линейное пространство, в котором введено скалярное произведение элементов, называют…. А) евклидовым пространством В) унитарным пространством С) линейной оболочкой D) подпространством E) арифметическим
202. Неравенство Коши – Буняковского, справедливое для двух любых элементов А) В) С) D) E)
203. Неравенство Минковского, справедливое для двух любых элементов А) В) С) D) E)
204. Норма любого элемента А) В) С) D) E)
205. Угол А) В) С) D) E)
206. Два произвольных элемента А) скалярное произведение этих элементов В) для С) скалярное произведение этих элементов D) не выполняется неравенство Коши - Буняковского E) для
207. А) эти элементы попарно ортогональны и норма каждого из элементов равна единице: В) эти элементы попарно ортогональны С) эти элементы попарно ортогональны и норма каждого из элементов больше единицы D) норма каждого из элементов равна единице E) эти элементы попарно ортогональны и норма каждого из элементов не равна единице
208. Матрица Грамма в евклидовом пространстве с заданным базисом А) В) С) D) E)
209. Матрица Грамма в ортонормированном базисе является … А) единичной.матрицей: В) нулевой матрицей С) столбцевой матрицей D) ортогональной матрицей E) треугольной матрицей
210. Квадратная матрица А) ортогональной матрицей В) ортоноромированной матрицей. С) столбцевой матрицей D) симметричной матрицей
|

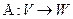 в паре базисов
в паре базисов 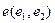 в
в 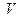 и
и 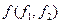 в
в 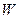 задан матрицей
задан матрицей 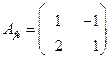 . Найдите координаты в базисе
. Найдите координаты в базисе 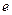
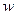 , заданного в базисе
, заданного в базисе 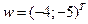 .
.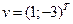
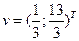
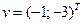

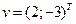
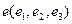 в
в  и
и 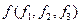 в
в 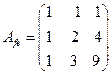 . Найдите координаты в базисе
. Найдите координаты в базисе 

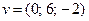
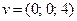
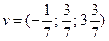
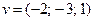
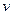 , удовлетворяющий соотношению
, удовлетворяющий соотношению 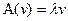 в линейном пространстве
в линейном пространстве 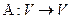 ?
?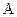 :
: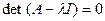
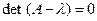
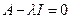
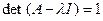 .
.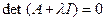
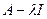 , где
, где 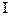 - тождественный оператор:
- тождественный оператор: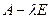

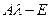
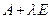 .
.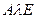
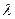 являлось собственным значением линейного оператора:
являлось собственным значением линейного оператора: линейного оператора
линейного оператора 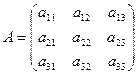 составьте характеристический многочлен матрицы
составьте характеристический многочлен матрицы 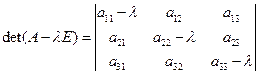
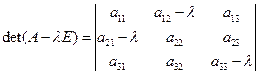
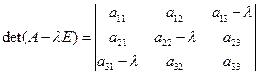
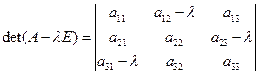
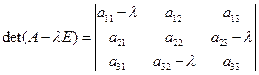
 :
: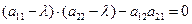
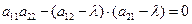
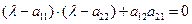 .
.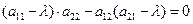

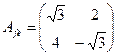 . Найдите координаты в базисе
. Найдите координаты в базисе  прообраза элемента
прообраза элемента 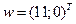
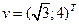
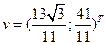
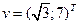
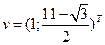
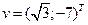
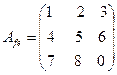 . Найдите координаты в базисе
. Найдите координаты в базисе 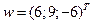 .
.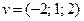
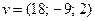
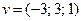
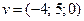
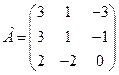
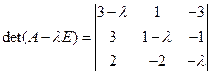
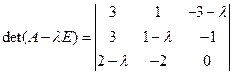

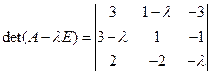
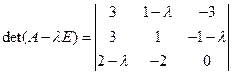
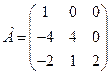 :
:
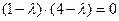
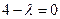 .
.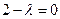

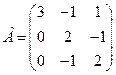


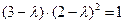 .
.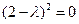
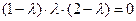
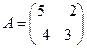 :
: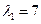 ,
, 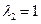
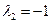 .
. ,
, 
 ,
, 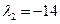
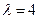

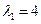 ,
, 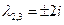 .
.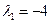 ,
, 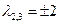
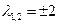
 линейного оператора
линейного оператора 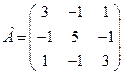 :
: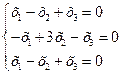
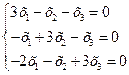
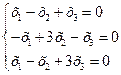 .
.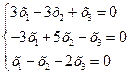
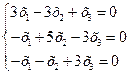
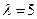 линейного оператора
линейного оператора 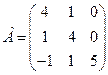 :
: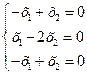
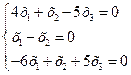
 .
.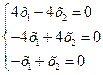
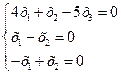
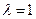 линейного оператора
линейного оператора 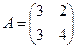
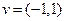
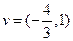
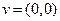
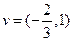
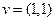
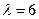 линейного оператора
линейного оператора 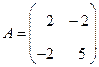
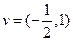
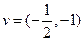
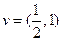
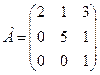 :
: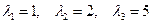
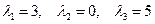
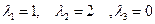
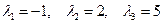
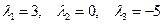
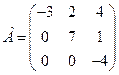 :
: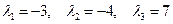

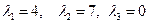
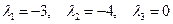
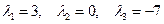
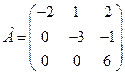 :
: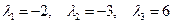
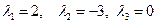
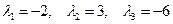
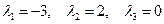
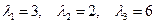
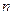 -мерным пространством
-мерным пространством и
и  произвольного евклидова пространства имеет вид…
произвольного евклидова пространства имеет вид…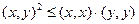

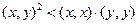
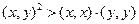

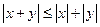
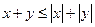
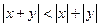
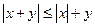
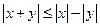

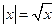
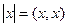
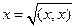
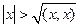
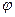 между элементами
между элементами 
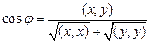
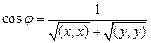
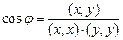
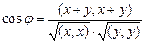
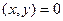
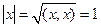 ,
, 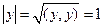
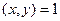
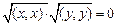
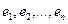
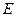 образуют ортонормированный базис этого пространства, если …
образуют ортонормированный базис этого пространства, если …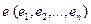 .имеет вид…
.имеет вид…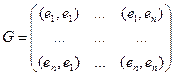
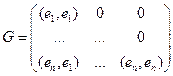
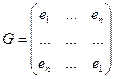
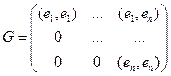
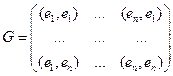
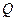 , для которой транспонированная матрица
, для которой транспонированная матрица 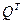 совпадает с обратной матрицей
совпадает с обратной матрицей 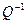 , называется …
, называется …


