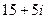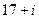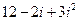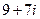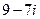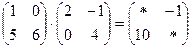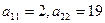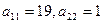Тестовое задание 7 страница
А) В) С) D) Е)
252. Определить величину параметра А) В) С) D) Е) 3
253. Определить координаты фокусов гиперболы А) В) С) D) Е)
254. Найти эксцентриситет А) В) С) D) Е)
255. В гиперболе оси равны А) В) С) D) Е)
256. Найти уравнение директрисы параболы А) В) С) D) Е)
257. Найти полуоси эллипса А) В) С) D) Е)
258. Составить каноническое уравнение гиперболы, если ее действительная полуось равна 8, а мнимая полуось равна 5 А) В) С) D) Е) 259. Эксцентриситет эллипса А) 14 В) 7 С) 10 D) 15 Е) 12
260. Определить величину параметра р параболы А) 2 В) 1 С) D) –1 Е) –2
261. Укажите общее уравнение плоскости в пространстве: A) B) C) D) E)
262. Укажите общее уравнение прямой в пространстве: A) B) C) D) E)
263. Укажите уравнение плоскости заданное точкой A) B) C) D) E)
264. Угол A) B) C) D) E)
265. Уравнение прямой в пространстве, проходящей через точки A) B) C) D) E)
266. Расстояние A) B) C) D) E)
267. Условие параллельности прямой A) B) C) D) E)
268. Условие перпендикулярности прямой A) B) C) D) E)
269. Каноническое уравнение прямой в пространстве имеет вид: A) B) C) D) E)
270. Определите координаты направляющего вектора A) B) C) D) E)
271. Дано уравнение плоскости A) B) C) D) E) Перпендикулярного к заданной плоскости вектора нет.
272. Дано уравнение плоскости A) B) C) D) E)
273. Уравнение плоскости, проходящей через точку A) B) C) D) E)
274 Общее уравнение плоскости,проходящей через точку A) B) C) D) E)
275. Составить канонические уравнения прямой, проходящей через точки A) B) C) D) E)
276. Составить параметрические уравнения прямой, проходящей через точку A) B) C) D) E)
277. Найти направляющий вектор A) B) C) D) E)
278. Найти угол A) B) C) D) E)
279. Найти угол A) B) C) D) E)
280. Найти расстояние A) B) C) D) E)
281. Укажите уравнение поверхности в пространстве A) B) C) D) E)
282. Уравнение сферы радиуса A) B) C) D) E)
283. Каноническое уравнение эллипсоида с центром в начале координат имеет вид A) B) C) D) E)
284. Определите поверхность второго порядка по ее геометрическому изображению A) однополостный гиперболоид B) двуполостный гиперболоид C) параболоид эллиптический D) конус эллиптический E) параболоид гиперболический
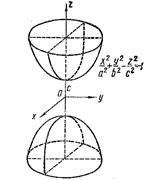
285. Определите поверхность второго порядка по ее геометрическому изображению A) двуполостный гиперболоид B) параболоид гиперболический C) параболоид эллиптический D) конус эллиптический E) однополостный гиперболоид
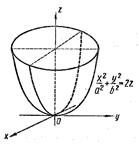
286. Определите поверхность второго порядка по ее геометрическому изображению A) параболоид эллиптический B) параболоид гиперболический C) однополостный гиперболоид D) конус эллиптический E) двуполостный гиперболоид
287. Уравнение цилиндрической поверхности с образующими, параллельными оси A) B) C) D) E)
288. Каноническое уравнение эллиптического цилиндра, направляющей линией которого является эллипс на плоскости A) B) C) D) E)
289. Каноническое уравнение гиперболического цилиндра, направляющей линией которого является гипербола на плоскости A) B) C) D) E)
290. Каноническое уравнение параболического цилиндра, направляющей линией которого является парабола на плоскости A) B) C) D) E)
291. Найти модуль комплексного числа A) B) C) D) E)
292. Найти модуль комплексного числа A) B) C) D) E)
293. Найти аргумент комплексного числа A) B) C) D) E)
294. Найти аргумент комплексного числа A) B) C) D) E)
295. Вычислить A) B) C) D) E)
296. Найти A) B) C) D) E)
297. Найти недостающие элементы произведения матриц А) B)
|

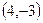
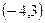
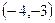
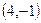
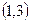
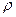 параболы
параболы 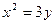 :
: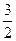
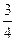
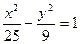 :
: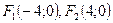
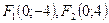
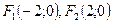
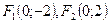
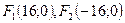
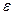 эллипса
эллипса 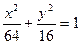 :
: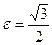
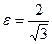
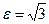
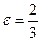
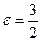
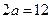 и
и 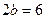 . Найти уравнения асимптот:
. Найти уравнения асимптот: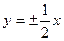
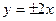
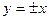
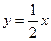
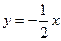
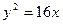 .
.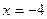

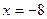
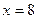
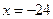
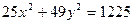 .
.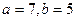
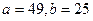
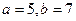
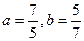
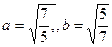
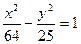
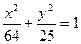
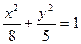
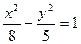
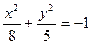
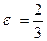 , большая полуось равна 7. Найти расстояние
, большая полуось равна 7. Найти расстояние 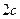 между фокусами:
между фокусами: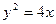 :
: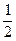
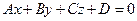
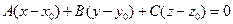
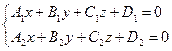
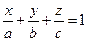

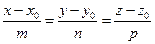
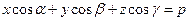
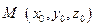 и нормальным вектором
и нормальным вектором 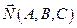 :
: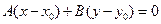
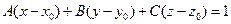
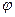 между прямой
между прямой 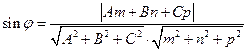
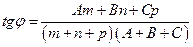
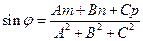
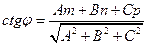
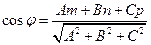
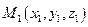 и
и 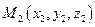 имеет вид:
имеет вид: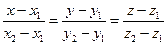
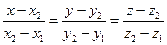
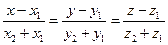

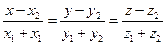
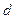 от точки
от точки 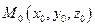 до плоскости
до плоскости 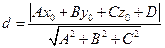
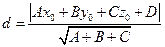
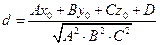
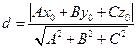
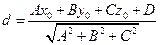
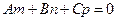
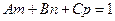
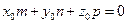
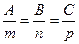
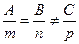

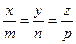
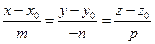
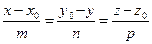
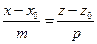
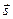 прямой в пространстве, если прямая задается общим уравнением прямой
прямой в пространстве, если прямая задается общим уравнением прямой 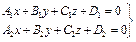
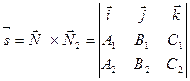
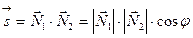 , где
, где 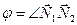
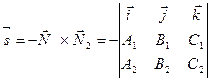
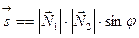 , где
, где 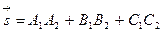
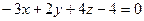 . Указать вектор, перпендикулярный заданной плоскости:
. Указать вектор, перпендикулярный заданной плоскости: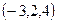
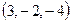
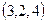
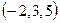
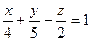 . Указать координаты точки пересечения данной плоскости с осью абсцисс:
. Указать координаты точки пересечения данной плоскости с осью абсцисс: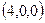
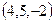
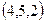

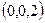
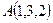 перпендикулярно вектору
перпендикулярно вектору 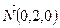 имеет вид:
имеет вид: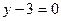
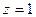
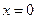
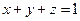
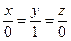
 перпендикулярно вектору
перпендикулярно вектору 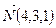 имеет вид:
имеет вид: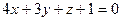
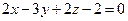
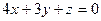
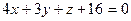
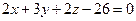
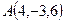 и
и 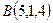 :
: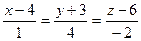
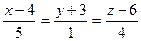

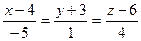
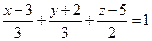
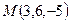 и параллельно вектору
и параллельно вектору 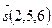 :
: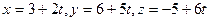
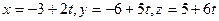
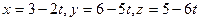
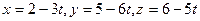
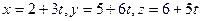
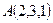 и
и 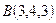 :
: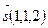
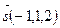
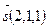
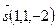
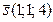
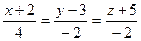 и плоскостью
и плоскостью 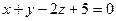 :
: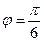
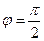
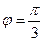
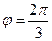
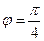
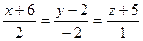 и плоскостью
и плоскостью 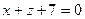 :
:
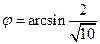
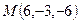 до плоскости
до плоскости  :
: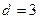
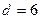
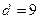
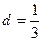
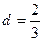
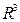 …
…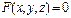
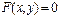
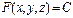
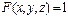
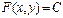
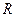 с центром в точке
с центром в точке 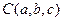 имеет вид
имеет вид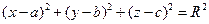
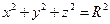
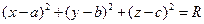
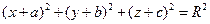
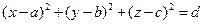
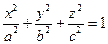
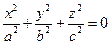
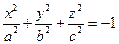
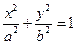

 ,имеет вид
,имеет вид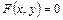
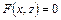

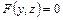
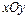 с полуосями
с полуосями  и
и 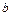
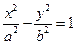
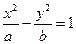
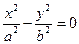
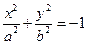
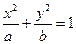
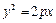
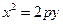
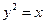
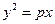
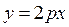
 :
: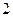
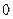
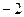
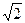
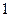
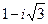 :
: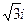
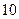
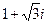
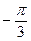
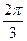
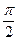
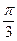
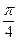
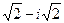 :
: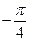
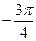
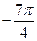
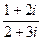 :
: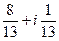
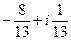
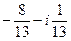
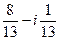
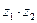 если
если 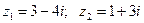 :
: