Центральна гранична теорема для однаково розподiлених незалежних випадкових величин.
Теорема. Якщо випадкові величини
тобто збігається до функції розподілу нормального закону. 3Рівномірна збіжніть є наслідком слабкої збіжності та неперервності нормального розподілу. Позначимо
Враховуючи, що
Остаточно
Наслідок(Інтегральна теорема Муавра-Лапласа) Якщо задана схема випробувань Бернуллі, а 3Розглянемо множину
|
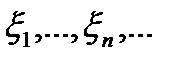є незалежними та однаково розподіленими і мають математичне сподівання 
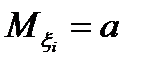, та скінчену дисперсію 
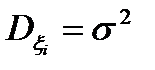, тоді
= 
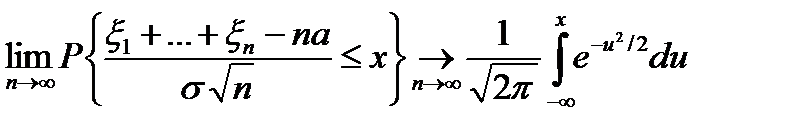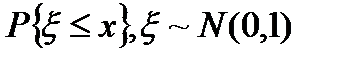
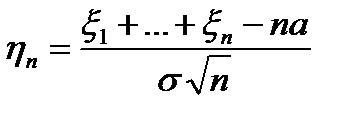і запишемо характеристичну функцію
- потрібно показати, що вона збігається до х.ф. нормального розподілу. Можна вважати, що а = 0 інакше можна було б розглянути 
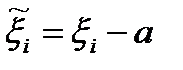- нові в.в. з мат. сподіванням, рівним 0, та 
.
, 
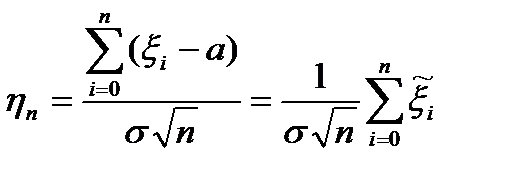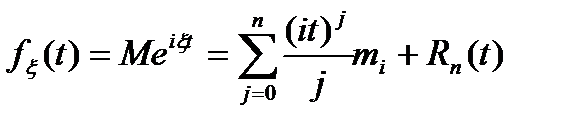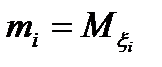. Оскільки існує 
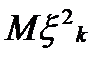, то справедливий розклад 
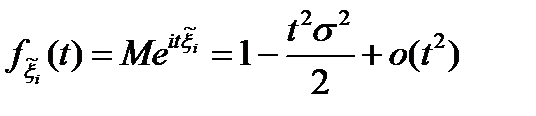. Крім того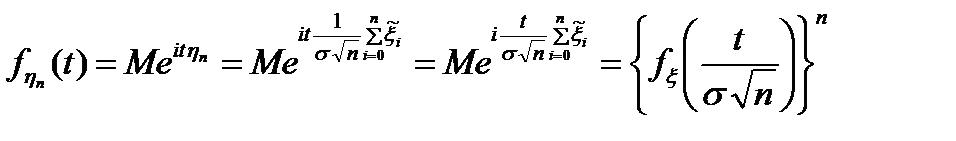
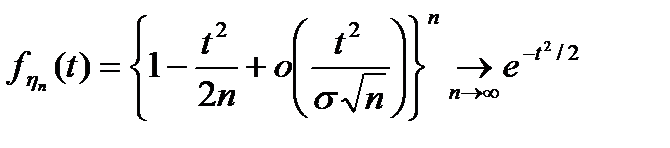, що і т.д.
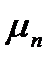- число успіхів у серії з n випробувань, то 
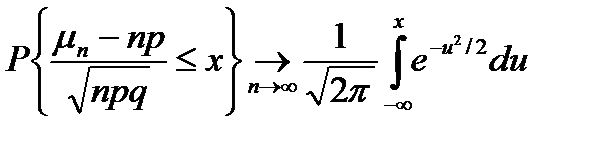- р ймовірність успіху
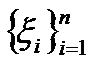кожна з яких має розподіл Бернуллі, тобто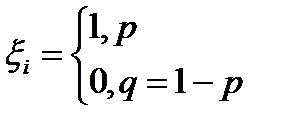 
, 
, 
.
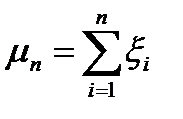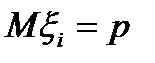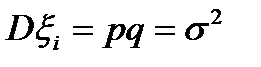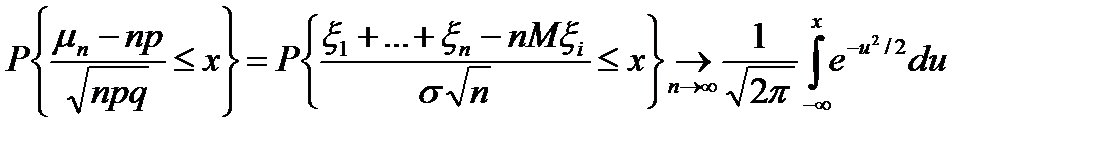4
