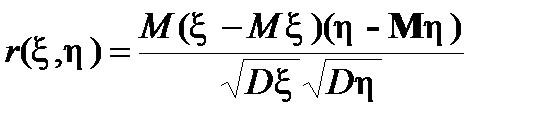Випадковi величини. Властивостi функцiй розподiлу.
Нехай маємо ймовірносний простір ( Озн.
Озн. Вимірна функція
Озн. F(x)= Властивості функцій розподілу. 1. F(x) – невід’ємна 2. F(x) - монотонно неспадна.(x1>=x2 => F(x1)>=F(x2))Справді:
3. F(x) - неперервна зліва. Тобто F(x-0) = F(x) 4. Нормованою F(- Дискретні випадкові величини. Нехай <W, Á,R>- ймовірнісний простір. Дискретноювипадковою величиною називається функція x(w) на W, яка набуває скінченне або зліченне число значень х1, х2, …, хn, … і є вимірною відносно s- алгебри Á. Це означає, що для кожного хі{ w: x(w)=x} ÎÁ (1).Дійсно, якщо для функції x(w) має місце співвідношення (1), то ця функція вимірна відносно Á, так як для кожного дійсного х { w: x(w)<x}= Функція розподілу дискретної випадкової величини x(w) визначається рівністю
Сумісний розподіл випадкових величинx(w) і h(w). Нехай x(w) – дискретна випадкова величина, яка набуває значень х1, х2,…, хі,…,h(w) – дискретна випадкова величина, яка набуває значень y1, y2,…, yі,…. Набір чисел Р{w:x(w)=xi, h(w)=yi}=pij(i=1, 2, …; j=1, 2, …) називається сумісним розподілом випадкових величин x і h (розподілом випадкового вектора (x, h)). Мають місце такі твердження: а) рij³0, б) Незалежні випадкові величини. Випадкові величини x і h P{x(w)=xi, h(w)= yi} = P{x(w)=xi} · P{h(w)= yi}. Математичне сподівання випадкової величини. Нехай x(w) – дискретна випадкова величина, яка набуває значень хі з імовірностямирі(і=1, 2, …). Припустимо, що ряд S½хі½рі збігається. Тоді м а т е м а т и ч н и м с п оді- в а н н я м випадкової величини x(w) називається сума ряду М x(w) = Дисперсія випадкової величини x(w) визначається рівністю Dx=M[x- Mx]2= Mx2-(Mx)2= Властивості дисперсії. 1. Dx=0 2. Dx= 3. D(Cx)=c2 Dx; 4. D(x 5. Якщо Коєфіцієнтковаріаціївипадкових величин Коефіцієнт кореляції. К о є ф і ц і є н т о м к о р е л я ц і ї випадкових величин x і h називаються
Мають місце такі твердження: а) ½r(x, h)½£ 1; б) якщо x і h незалежні, то r(x, h)=0; в) якщо ½r(x, h)½=1, то з імовірністю одиниця h=аx+b, де а і b – деякі сталі.
|

 , F, P).
, F, P). 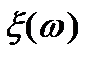 - деяка функція, визначена на
- деяка функція, визначена на 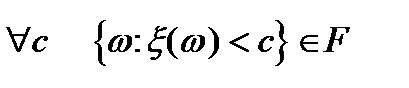 , де F
, де F 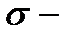 алгебра.
алгебра.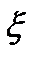 - випадкова величина,
- випадкова величина,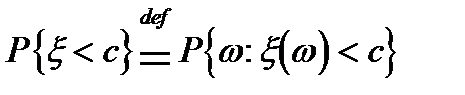 .
.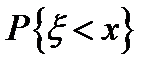 - функція розподілу випадкової величини
- функція розподілу випадкової величини  .
.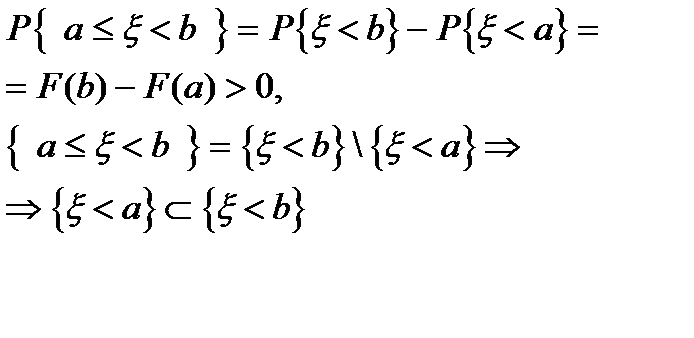 Отже
Отже ) = 0, F(+
) = 0, F(+ 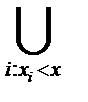 { w: x(w)=xі} ÎÁ. Крім того, якщо x(w) вимірна відносно s- алгебри Á, то за Теоремою 1 для кожного дійсного х { w: x(w)=x } ÎÁ. Таким чином, якщо x(w)- дискретна випадкова величина на ймовірнісному просторі <W, Á,R>, яка приймає значення х1, х2, …, хn, …, то для кожного n визначена ймовірність Рn=Р{ w: x(w)=xn} Нехай x(w) – дискретна випадкова величина, яка набуває значення х1,…, хі,…. Набір чисел Р{w:x(w)=xi}=pi(i=1,2,…) називають розподілом випадкової величини x. Зрозуміло, що рі³ 0,
{ w: x(w)=xі} ÎÁ. Крім того, якщо x(w) вимірна відносно s- алгебри Á, то за Теоремою 1 для кожного дійсного х { w: x(w)=x } ÎÁ. Таким чином, якщо x(w)- дискретна випадкова величина на ймовірнісному просторі <W, Á,R>, яка приймає значення х1, х2, …, хn, …, то для кожного n визначена ймовірність Рn=Р{ w: x(w)=xn} Нехай x(w) – дискретна випадкова величина, яка набуває значення х1,…, хі,…. Набір чисел Р{w:x(w)=xi}=pi(i=1,2,…) називають розподілом випадкової величини x. Зрозуміло, що рі³ 0, 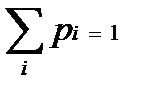 .
.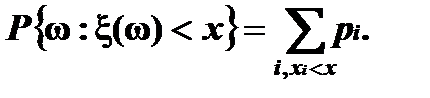

 де {pi} розподіл x(w), {qi} – розподіл h(w).
де {pi} розподіл x(w), {qi} – розподіл h(w).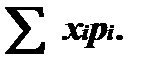 Якщо S½хі½рі=+¥, то кажуть, що випадкова величина x(w) не має математичного сподівання. Математичне сподівання суми випадкових величин дорівнює сумі математичних сподівань.
Якщо S½хі½рі=+¥, то кажуть, що випадкова величина x(w) не має математичного сподівання. Математичне сподівання суми випадкових величин дорівнює сумі математичних сподівань.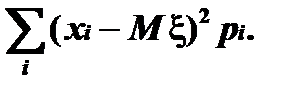
 x=соnst;
x=соnst;
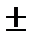 C)= Dx.
C)= Dx.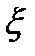 та
та  незалежні випадкові величини, то D(
незалежні випадкові величини, то D(