Поняття випадкового процесу. Вiнерiвський та Пуасонiвський процеси.Озн. Випадковий процес - це система в.в. У ТЙ: ВП - множина в.в. Класифікація ВП: 1) за типом а) У цьому випадку ВП - це послідовність в.в. б) 2) За типом множини значень:
3) За способом опису спільних розподілів Множину значень називають також множиною можливих станів.
Озн. 1)Процесом з незалежними приростами називається випадковий процес, визначенийй для 2) Однорідні ПНП - це процеси, у яких: а) б) розподіл 3) Стохастично-неперервні ОПНП - це такі, у яких Характеристична функція для с/н ОПНП Із властивостей характеристичних функцій випливає, що
Теорема Характеристична функція с/н ОПНП представляється у вигляді Висновок: для задання с/н ОПНП необхідно і достатньо задати кумулянту Теорема. (Про представлення кумулянти) Кумулянта представляється у вигляді:
|
, 
, 
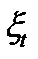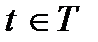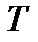- проміжок часу, яка описує еволюцію процесу, що досліджується,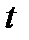 
, визначена на одному і тому ж імовірністному просторі 
. 
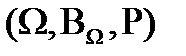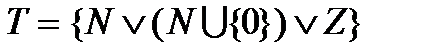- процеси з дискретним часом.
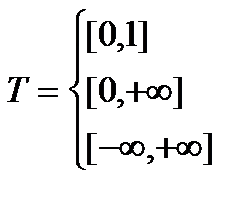- процеси з неперервним часом.
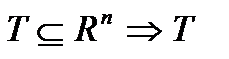- поле
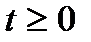із дискретною або неперервною множиною станів, для якого виконується умова: для будь-якого скінченого набору моментів часу 
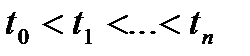випадкові величини 
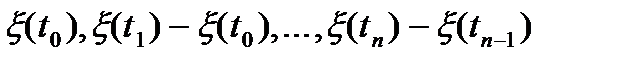- незалежні.
;
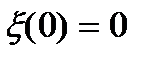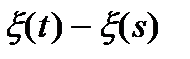залежить тільки від 
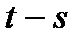, тобто співпадає з розподілом 
.
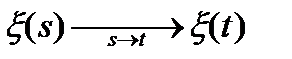, тобто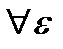 
, 
.
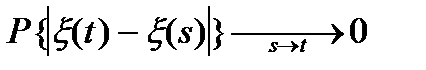
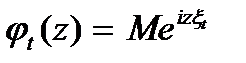
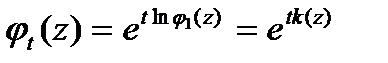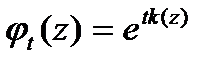, де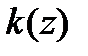 
- кумулянта процесу.
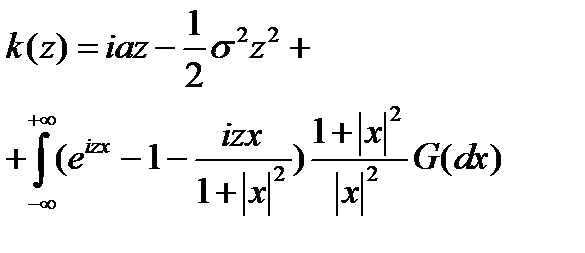, де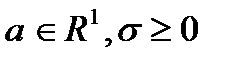 
, 
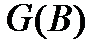- скінчена міра, що не має атома в нулі: 
.
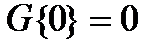