Цей критерій застосовується для перевірки гіпотез типу 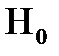 , які мають форму припущення про вигляд функції розподілу.
, які мають форму припущення про вигляд функції розподілу.
Маємо вибірку з геральної сукупності 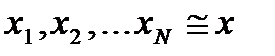
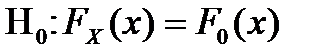 , де
, де 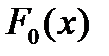 - будь-яка задана, тобто функція розподілу
- будь-яка задана, тобто функція розподілу  перевіряється на співпадання з заданою.
перевіряється на співпадання з заданою.
Алгоритм критерію:
1. Будуємо статистику  , де
, де 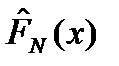 - емпірична функція розподілу. Тоді справедлива
- емпірична функція розподілу. Тоді справедлива
Теорема. (Колмогорова).
Якщо вибірка була побудована з функцією розподілу 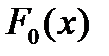 (
(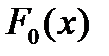 повинна бути неперервною), тобто має місце наше припущення, то
повинна бути неперервною), тобто має місце наше припущення, то
 . Тобто якщо припущення зроблено не правильно, то данної границі, взагалі кажучи, може не існувати.
. Тобто якщо припущення зроблено не правильно, то данної границі, взагалі кажучи, може не існувати.
2. По вибранному 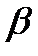 знаходимо
знаходимо  :
:  , далі
, далі  - довірча область для
- довірча область для  .
.
3. Приймаємо рішення в залежності від справедливості співвідношення:  : + -
: + - 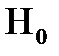 приймається
приймається
- - 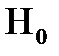 відхиляється
відхиляється

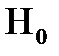 , які мають форму припущення про вигляд функції розподілу.
, які мають форму припущення про вигляд функції розподілу.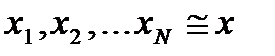
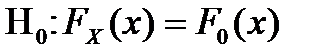 , де
, де 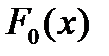 - будь-яка задана, тобто функція розподілу
- будь-яка задана, тобто функція розподілу  перевіряється на співпадання з заданою.
перевіряється на співпадання з заданою. , де
, де 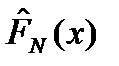 - емпірична функція розподілу. Тоді справедлива
- емпірична функція розподілу. Тоді справедлива . Тобто якщо припущення зроблено не правильно, то данної границі, взагалі кажучи, може не існувати.
. Тобто якщо припущення зроблено не правильно, то данної границі, взагалі кажучи, може не існувати.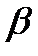 знаходимо
знаходимо  :
:  , далі
, далі  - довірча область для
- довірча область для  .
. : + -
: + - 


