Говорять, що послідовність випадкових величин 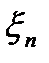 , по ймовірності збігається до випадкової величини
, по ймовірності збігається до випадкової величини 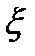 , якщо для довільного
, якщо для довільного 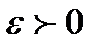
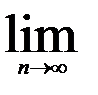 Р {
Р { 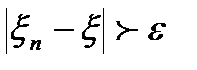 }=0. Збіжність по ймовірності послідовності
}=0. Збіжність по ймовірності послідовності 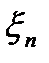 до
до 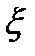 позначають так:
позначають так: 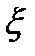 =plim
=plim 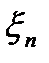 , або
, або 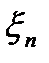
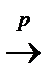
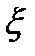 .
.
Нехай 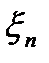 послідовність випадкових величин, для яких існують М
послідовність випадкових величин, для яких існують М 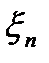 . Законом великих чисел називають теореми, які стверджують, що різниця
. Законом великих чисел називають теореми, які стверджують, що різниця 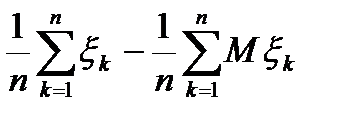 збігається до нуля по ймовірності.
збігається до нуля по ймовірності.
Нерівність Чебишева:
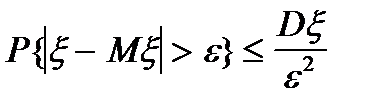 , де
, де 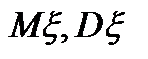 - математичне сподівання та дисперсія в.в.
- математичне сподівання та дисперсія в.в. 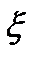 відповідно.
відповідно.
Теорема Чебишова. Нехай { 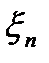 }- послідовність незалежних випадкових величин, існують D
}- послідовність незалежних випадкових величин, існують D 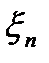 i D
i D 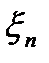
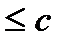 при всіх n. Тоді
при всіх n. Тоді 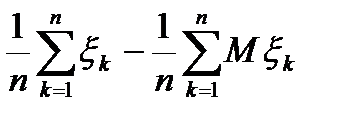
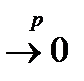 . (*)
. (*)
Наслідок. Нехай 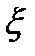 1,
1, 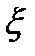 2,…,
2,…, 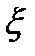 n,…- послідовність незалежних випадкових величин така, що М
n,…- послідовність незалежних випадкових величин така, що М 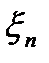 =а, D
=а, D 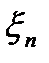
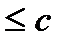 , n=1,2,…
, n=1,2,…
Тоді для кожного 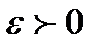
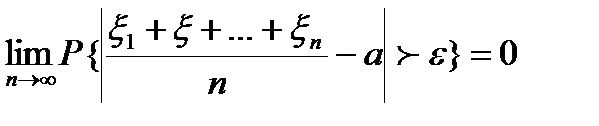 .
.
Цей частковий випадок теореми Чебишова дає обгрунтуваня правилу середнього арифметичного в теорії обробки результатів вимірювання. Припустимо, що необхідно виміряти деяку фізичну величину а. Повторюючи вимірювання n раз в одинакових умовах, спостерігач одержує результати вимірювань 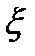 1,
1, 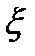 2,…,
2,…, 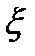 n [1]. Якщо спостереження не мають систематичної помилки, тобто М
n [1]. Якщо спостереження не мають систематичної помилки, тобто М 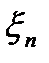 =а, то згідно сформульованому вище наслідку,
=а, то згідно сформульованому вище наслідку, 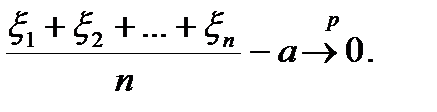
Теорема Хінчина. Нехай { 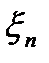 }- послідовність незалежних одинаково розподіленихвеличин, які мають скінчене математичне сподівання М
}- послідовність незалежних одинаково розподіленихвеличин, які мають скінчене математичне сподівання М 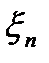 =а. Тоді для кожного
=а. Тоді для кожного 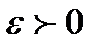
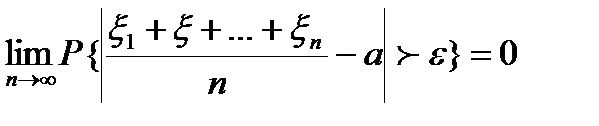 .
.
Теорема Маркова. Нехай випадкові величини 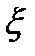 1,
1, 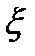 2,…,
2,…, 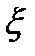 nякзавгодно залежні. Для виконання (*) достатньо, щоб
nякзавгодно залежні. Для виконання (*) достатньо, щоб
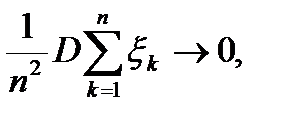 при
при 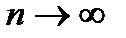 .
.
Теорема Бернуллі. Нехай маємо послідовність випробовувань, в кожному з яких можуть бути два наслідки- успіх У (з ймовірністю р) або невдача Н (з ймовірністю q=1-p) незалежно від наслідків інших випробувань. Утворимо послідовність випадкових величин наступним чином. Нехай 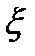 к =1, якщо в к-тому випробовуванні був успіх
к =1, якщо в к-тому випробовуванні був успіх 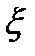 к =0, якщо в к-тому випробовуванні наступила невдача. Тоді {
к =0, якщо в к-тому випробовуванні наступила невдача. Тоді { 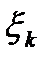 }- є послідовність незалежних одинаково розподілених випадкових величин M
}- є послідовність незалежних одинаково розподілених випадкових величин M 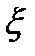 к=p, D
к=p, D 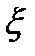 к=pq. Випадкова величина
к=pq. Випадкова величина 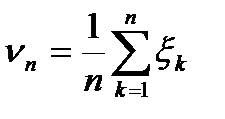 представляє собою частоту появи успіху в перших n випрбуваннях. Оскільки для послідовності {
представляє собою частоту появи успіху в перших n випрбуваннях. Оскільки для послідовності { 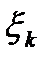 }-виконані умови теореми Чебишова, то із теореми Чебишова одержуємо наступне твердження.
}-виконані умови теореми Чебишова, то із теореми Чебишова одержуємо наступне твердження.
Теорема Бернуллі. Для довільного 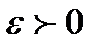 Р{
Р{ 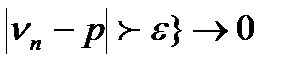 при n
при n 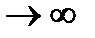 .
.
Зміст цього твердження полягає в тому, що ведене нами визначення ймовірності відповідає інтуїтивному розумінню ймовірності як границі частоти.
Теорема. Нехай 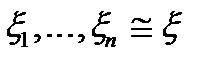 - незалежні однаково розподілені випадкові величини, причому
- незалежні однаково розподілені випадкові величини, причому 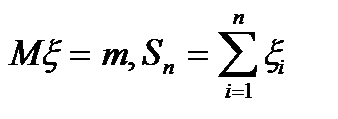 , тоді
, тоді 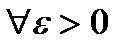
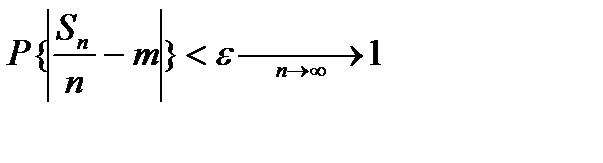 .
.
Закон великих чисел є математичниимпідгрунтям для частотного визначення математичного сподівання як інтегральної характеристики розподілу: 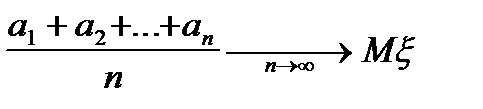 .
.

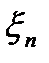 , по ймовірності збігається до випадкової величини
, по ймовірності збігається до випадкової величини 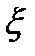 , якщо для довільного
, якщо для довільного 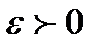
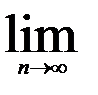 Р {
Р { 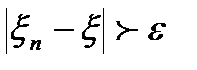 }=0. Збіжність по ймовірності послідовності
}=0. Збіжність по ймовірності послідовності 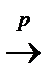
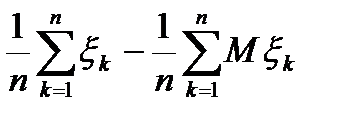 збігається до нуля по ймовірності.
збігається до нуля по ймовірності.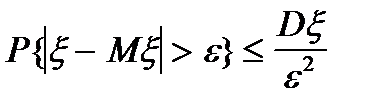 , де
, де 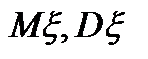 - математичне сподівання та дисперсія в.в.
- математичне сподівання та дисперсія в.в. 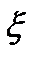 відповідно.
відповідно.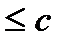 при всіх n. Тоді
при всіх n. Тоді 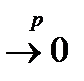 . (*)
. (*)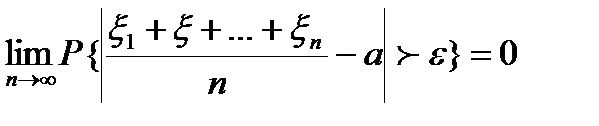 .
.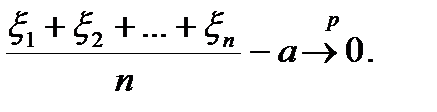
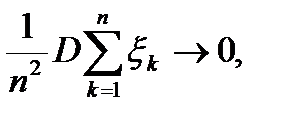 при
при 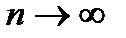 .
.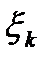 }- є послідовність незалежних одинаково розподілених випадкових величин M
}- є послідовність незалежних одинаково розподілених випадкових величин M 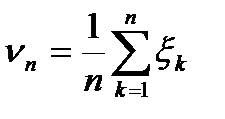 представляє собою частоту появи успіху в перших n випрбуваннях. Оскільки для послідовності {
представляє собою частоту появи успіху в перших n випрбуваннях. Оскільки для послідовності { 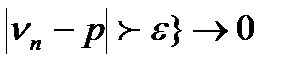 при n
при n 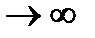 .
.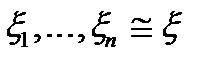 - незалежні однаково розподілені випадкові величини, причому
- незалежні однаково розподілені випадкові величини, причому 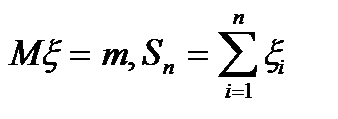 , тоді
, тоді 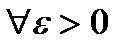
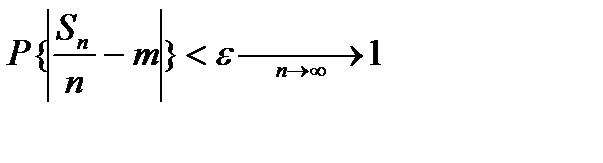 .
.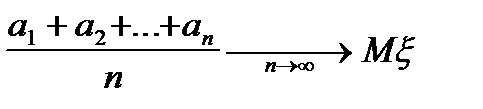 .
.


