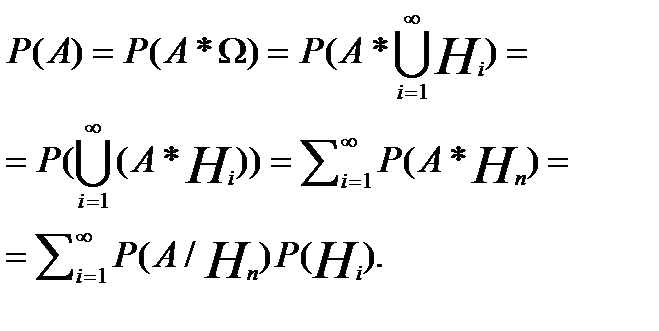Аксiоматичне означення ймовiрностей. Формула повної ймовiрностi та формула Байеса.
Теорiя ймовiрностей та математична статистика 1. Аксiоматичне означення ймовiрностей. Формула повної ймовiрностi та формула Байеса. 2. Випадковi величини. Властивостi функцiй розподiлу. 3. Нерiвнiсть Чебишева. Закон великих чисел. 4. Основнi типи дискретних та неперервних розподiлiв. 5. Центральна гранична теорема для однаково розподiлених незалежних випадкових величин. 6. Поняття випадкового процесу. Вiнерiвський та Пуасонiвський процеси. 7. Випадкове середнє та дисперсiя. Емпiрична функцiя розподiлу. Теореми Глiвенка та Колмогорова. 8. Перевiрка статистичних гiпотез. Критерiї Колмогорова та Пiрсона.
Аксiоматичне означення ймовiрностей. Формула повної ймовiрностi та формула Байеса. Спочату введемо кілька допоміжних понять. Озн. Множина U є алгеброю, якщо 1) 2) 3). Озн. Множина U є 1) 2) 3). Будемо вважати, що множина всіх подій утворює Озн. Числову функцію, задану на множині всіх подій U, будемо називати ймовірністю, якщо 1. Р(А) 2. Р( 3. Озн. Ймовірносний простір- це трійка об’єктів: ( Озн. Під аксіоматикою теорії ймовірності розуміють три властивості, накладені на U, і три властивості накладені на Р. Відомо ряд важливих наслідків з цих властивостей, які легко доводяться. Приведемо їх. 1. Якщо 2. 3. P( 4. P( 5. Неперервність зверху: Озн. Умовною ймовірністю прийнято називати величину Р(А/В)= Озн. А і В - незалежні події, якщо Р( Озн. Кажуть, що Формула повної ймовірності має вигляд, якщо
Формула Баєса відповідно має вигляд (при тих же припущеннях)
|

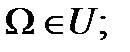
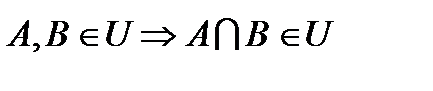 і
і 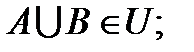
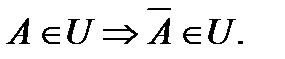
 - алгеброю, якщо
- алгеброю, якщо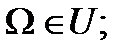
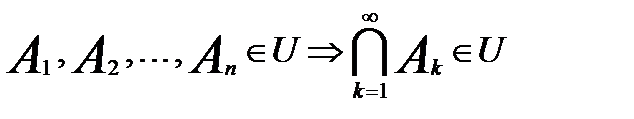 і
і 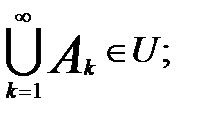
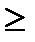 0;
0; )=1; Р(
)=1; Р(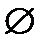 )=0;
)=0;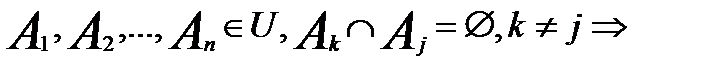
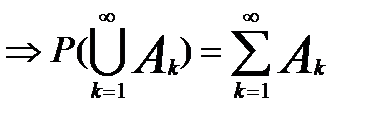 .
.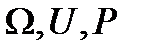 ).
).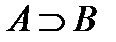 , то
, то 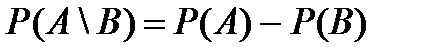 .
.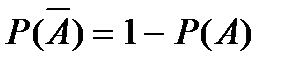 .
.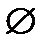 )= 0.
)= 0.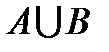 )=P(A)+P(B)-P(
)=P(A)+P(B)-P(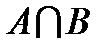 ),
), 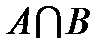
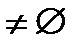 .
.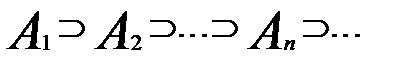 і
і 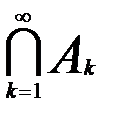 =
= 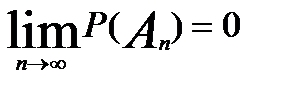 .
.
 )=Р(А)Р(В).
)=Р(А)Р(В). утв-ють повну групу подій, якщо
утв-ють повну групу подій, якщо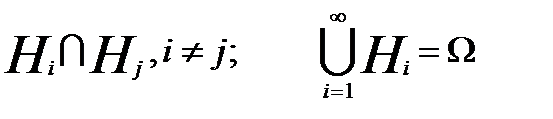 .
.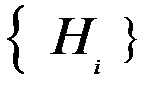 - повна група подій,
- повна група подій,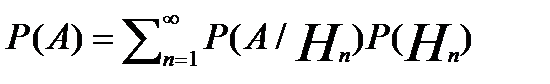 . Дійсно
. Дійсно