У задачі перевірки гіпотез типу АВ формулюються два припущення, щодо можливості значення невідомого параметру  . Ці припущення позначаються як
. Ці припущення позначаються як 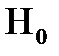 та
та 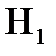 . На основі виборки
. На основі виборки  , треба сформулювати правило, яке б робило вибір на користь тієї чи іншої гіпотези.
, треба сформулювати правило, яке б робило вибір на користь тієї чи іншої гіпотези.
Оскільки кожна серія спостережень дає нову вибірку,то висновки про ту чи іншу гіпотезу (що базуються на основі правила) будуть носити випадковий характер. Отже, в задачі АВ вводять додаткову характеристику: довірчу ймовірність 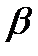 - ймовірність прийняття гіпотези
- ймовірність прийняття гіпотези 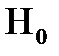 , коли вона є справедливою.
, коли вона є справедливою.
Більш формально: 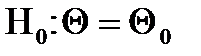 ,
,  ,
, 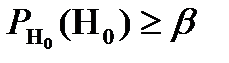 ,
, 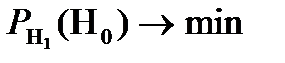 .
.
В задачі АВ необхідно з двох однотипних припущень 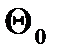 та
та  про значення параметру
про значення параметру  вибрати одне. Ймовірність вибору першого, коли воно дійсно вірне, повинна бути
вибрати одне. Ймовірність вибору першого, коли воно дійсно вірне, повинна бути  , а також ймовірність відхилення другого, якщо насправді воно справедливе, повинна бути мінімальною. Ці дві ймовірності в математичній статистиці прийнято називати похибками першого та другого роду відповідно. Тобто необхідно прийняти рішення при фіксованій похибці першого роду і так, щоб похибка другого роду була мінімальною.
, а також ймовірність відхилення другого, якщо насправді воно справедливе, повинна бути мінімальною. Ці дві ймовірності в математичній статистиці прийнято називати похибками першого та другого роду відповідно. Тобто необхідно прийняти рішення при фіксованій похибці першого роду і так, щоб похибка другого роду була мінімальною.
Типу.
У задачі перевірки гіпотези типу 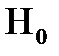 висувається наступна гіпотеза:
висувається наступна гіпотеза: 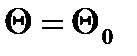 і її альтернатива:
і її альтернатива:  . Отже у цьому типі гіпотез на відміну від попередньго випадку, основна гіпотеза
. Отже у цьому типі гіпотез на відміну від попередньго випадку, основна гіпотеза 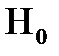 і альтернативна
і альтернативна  є різними за типом:
є різними за типом: 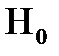 - одинична та
- одинична та  - множинна.
- множинна.
Отже в цій задачі треба із імовірністю 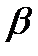 підтвердити припущення
підтвердити припущення 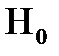 , коли воно є вірним чи відхилити його.
, коли воно є вірним чи відхилити його.

 . Ці припущення позначаються як
. Ці припущення позначаються як 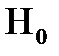 та
та 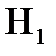 . На основі виборки
. На основі виборки  , треба сформулювати правило, яке б робило вибір на користь тієї чи іншої гіпотези.
, треба сформулювати правило, яке б робило вибір на користь тієї чи іншої гіпотези.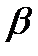 - ймовірність прийняття гіпотези
- ймовірність прийняття гіпотези 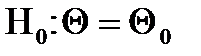 ,
,  ,
, 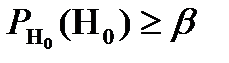 ,
, 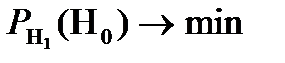 .
.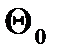 та
та  про значення параметру
про значення параметру  , а також ймовірність відхилення другого, якщо насправді воно справедливе, повинна бути мінімальною. Ці дві ймовірності в математичній статистиці прийнято називати похибками першого та другого роду відповідно. Тобто необхідно прийняти рішення при фіксованій похибці першого роду і так, щоб похибка другого роду була мінімальною.
, а також ймовірність відхилення другого, якщо насправді воно справедливе, повинна бути мінімальною. Ці дві ймовірності в математичній статистиці прийнято називати похибками першого та другого роду відповідно. Тобто необхідно прийняти рішення при фіксованій похибці першого роду і так, щоб похибка другого роду була мінімальною.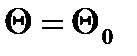 і її альтернатива:
і її альтернатива:  . Отже у цьому типі гіпотез на відміну від попередньго випадку, основна гіпотеза
. Отже у цьому типі гіпотез на відміну від попередньго випадку, основна гіпотеза  є різними за типом:
є різними за типом: 


