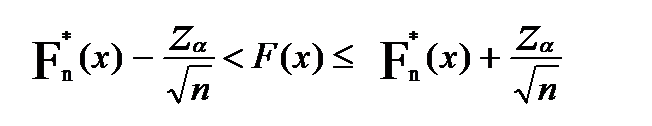Випадкове середнє та дисперсiя. Емпiрична функцiя розподiлу. Теореми Глiвенка та Колмогорова.
Озн. Вибірка - мат. модель незалежних вимірювань, що проводяться в однакових умовах. Основною характеристикою вибірки є емпірична функція розподілу. Озн. Емпірична функція розподілу - це функція вигляду
інакше кажучи, це сума тих елементів вибірки, поділена на n, які попали лівіше,ніж n. Очевидно, що ця функція також випадкова. Озн. Варіаційний ряд- елементи вибірки, розміщені в порядку зростання:
Озн. Кажуть, що послідовність випадкових величин
Має місце слідуюча теорема: Теорема. Якщо F(x) - теоретична функція розподілу, то справедливе наступне твердження:
Доведення. Нехай xk - довільний елемент вибірки. Розглянемо множини р Тоді для кожного x емпірична функція розподілу буде показувати кількість успіхів, поділену на n, в схемі Бернуллі з n випробуваннями та характеристиками p та q. Далі, за законом великих чисел в схемі Бернуллі маємо
Все. Озн. Вибірковий момент 1-го порядку - вибіркове середнє визначається для вибірки з генеральної сукупності за формулою:
Також мають місце слідуючі важливі теореми. Теорема Глівенка. Для довільної функції розподілу справедливе твердження
Теорема Колмогорова. Для довільної неперервної функції розподілу F(x) справедливе наступне твердження:
де K(z) - функція розподілу Колмогорова. Тобто K(z)= Тобто якщо задати якесь значення
|
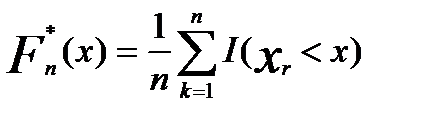, де 
.
збігається за ймовірністю до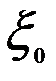 
, якщо
,
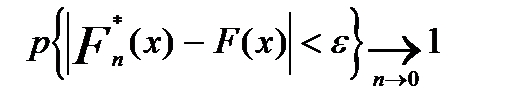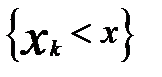та 
.
.
та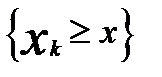 
. В схемі Бернуллі
, що і доводить теорему.
, а вибіркова дисперсія - центрований момент 2-го порядку:
2.
.
,
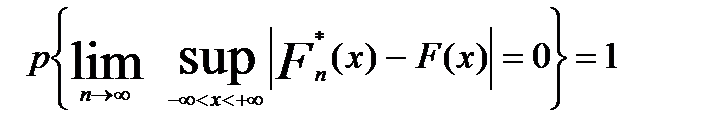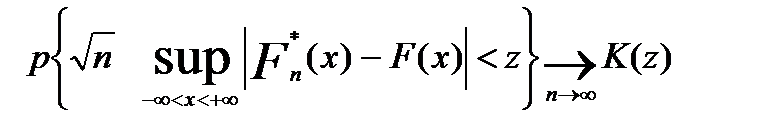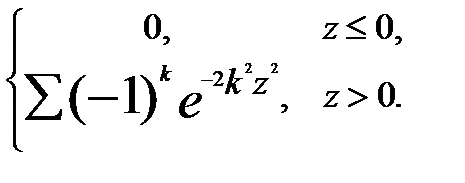
і підібрати таке 
, що К(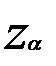
)= 
