Ветряной оспой населения в городе Б.
| Годы
|
|
|
|
|
|
| | А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| | Средние данные за 9 лет (а)
| 225,6
| 137,6
| 185,6
| 113,2
| 171,6
| 104,6
| 167,4
| 102,1
| 140,0
| 85,4
| 99,0
| 60,4
| | Медиана (б)
| 230,0
| 137,0
| 173,2
| 101,3
| 156,3
| 98,4
| 176,5
| 110,9
| 131,7
| 84,8
| 105,8
| 60,4
| | Средние данные за неблаго-получные годы (в)
| 252,5
| 155,1
| 213,8
| 131,3
| 198,3
| 121,8
| 173,3
| 106,4
| 142,3
| 87,4
| 102,6
| 63,0
| | Средние данные за благо-получные годы (г)
| 171,7
| 103,3
| 129,2
| 77,7
| 118,0
| 71,0
| 155,5
| 93,6
| 135,4
| 81,4
| 91,9
| 55,3
| Продолжение табл. 17
| Годы
|
|
|
|
|
|
| Итого
| | А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| | а
| 59,1
| 36,0
| 41,6
| 25,4
| 46,7
| 33,7
| 106,6
| 65,0
| 164,8
| 100,5
| 206,0
| 125,7
| 1613,9
| 984,4
| | б
| 54,0
| 35,3
| 42,1
| 25,4
| 56,3
| 34,6
| 96,5
| 50,7
| 159,6
| 100,9
| 204,8
| 112,7
| 1586,8
| 967,8
| | в
| 61,3
| 37,6
| 40,8
| 25,0
| 59,6
| 36,6
| 125,1
| 76,8
| 199,2
| 122,4
| 239,4
| 147,0
| 1808,1
| 1110,6
| | г
| 54,7
| 32,9
| 43,3
| 26,0
| 46,8
| 28,1
| 69,6
| 41,9
| 95,8
| 57,6
| 139,3
| 83,8
| 1251,2
| 752,6
| Б. Схема корригирования показателей заболеваемости при криволинейной эпидемической тенденции:
1. Выравнивание годовых показателей заболеваемости (по параболе 2-го или 3-го порядка либо другим методом) с расчетом I теоретического (табл. 18, рис. 17):
 ; ;  ; ; 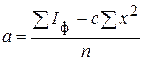 ; ;  ; ;
b = -6,9; a = 19,2; c = 2,6.
Участок кривой эпидемической тенденции продолжительностью в один год условно можно рассматривать как отрезок прямой. Крайними координатами этого отрезка являются интенсивные теоретические показатели (I T) за два смежные года. Разница между этими показателями соответствует коэффициенту b при прямолинейной тенденции. Таким образом, по аналогии с предыдущим расчетом корригирующего коэффициента, К для каждого конкретного года равен разнице I T данного и предыдущего годов, деленной на 144, т.е.:
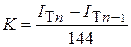 . .
Теоретическое значение (I T ) для года, предшествующего первому анализируемому году, рассчитывается по формуле для I теоретического с подстановкой соответствующего х (табл. 19).
2. Корригирование месячных показателей заболеваемости за каждый анализируемый год: от показателя за январь отнимают 0·К, за февраль – 1·К, за март 2·К и так далее до декабря – 11·К (см. табл. 19; табл. 20). Если корригированный месячный показатель оказывается отрицательным числом – его заменяют на ноль.
IV (III). Определение среднемноголетних показателей заболеваемости за каждый месяц, медианы, среднемноголетних месячных показателей заболеваемости за годы эпидемического благополучия и неблагополучия (см. табл. 20).
Таблица 18
Многолетняя эпидемическая тенденция заболеваемости вирусным гепатитом А населения в городе В. по параболе 2-го порядка
| Год
| IФ
| х
| х2
| x4
| xIФ
| x2I
| IT
| (ITn-ITn-1)
| К
| N
| КА
| |
|
| -5
|
|
|
|
| 118,8
|
|
|
|
| |
| 80,3
| -4
|
|
| -321,2
| 1284,8
| 88,5
| -30,3
| -0,21
|
| -0,57
| |
| 71,3
| -3
|
|
| -213,9
| 641,7
| 63,3
| -25,1
| -0,17
|
| -0,47
| |
| 48,4
| -2
|
|
| -96,8
| 193,6
| 43,4
| -19,9
| -0,14
|
| -0,36
| |
| 27,6
| -1
|
|
| -27,6
| 27,6
| 28,7
| -14,7
| -0,10
|
| -0,27
| |
| 19,3
|
|
|
|
|
| 19,2
| -9,5
| -0,07
|
| -0,17
| |
| 15,1
|
|
|
| 15,1
| 15,1
| 14,9
| -4,3
| -0,03
|
| -0,08
| |
| 11,7
|
|
|
| 23,4
| 46,8
| 15,8
| 0,9
| 0,01
|
| 0,02
| |
| 14,1
|
|
|
| 42,3
| 126,9
| 21,9
| 6,1
| 0,04
|
| 0,11
| |
| 41,2
|
|
|
| 164,8
| 659,2
| 33,3
| 11,3
| 0,08
|
| 0,19
| 
| 329,0
|
|
|
| -413,9
| 2995,7
|
|
|
|
|
|  V. Построение типовой и групповых кривых годовой динамики заболеваемости, т.е. графическое изображение сезонных колебаний. Для этих целей используют линейные (рис. 18, 19) и радиально-круговые диаграммы (рис. 20, 21). V. Построение типовой и групповых кривых годовой динамики заболеваемости, т.е. графическое изображение сезонных колебаний. Для этих целей используют линейные (рис. 18, 19) и радиально-круговые диаграммы (рис. 20, 21).
Таблица 19
Годовая динамика заболеваемости вирусным гепатитом А в городе В.
| Годы
|
|
|
|
|
|
|
|
|
|
|
|
| Итого
| | А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| А
| І
| |
|
| 7,4
|
| 6,3
|
| 3,0
|
| 1,9
|
| 4,1
|
| 2,6
|
| 2,2
|
| 3,0
|
| 8,9
|
| 13,4
|
| 13,8
|
| 13,0
|
| 79,7
| |
|
| 7,4
|
| 8,5
|
| 5,6
|
| 3,3
|
| 3,0
|
| 2,6
|
| 1,9
|
| 4,5
|
| 7,4
|
| 8,9
|
| 9,3
|
| 6,7
|
| 69,1
| |
|
| 3,8
|
| 1,9
|
| 4,2
|
| 4,9
|
| 1,5
|
| 3,0
|
| 1,1
|
| 4,6
|
| 11,0
|
| 6,5
|
| 5,3
|
| 3,8
|
| 51,7
| |
|
| 0,8
|
| 1,9
|
| 1,9
|
| 1,9
|
| 1,2
|
| 1,5
|
| 1,5
|
| 3,5
|
| 6,2
|
| 1,5
|
| 3,1
|
| 2,7
|
| 27,7
| |
|
| 1,5
|
| 0,4
|
| 1,5
|
| 1,9
|
| 1,5
|
| 0,8
|
| 3,1
|
| 2,3
|
| 1,5
|
| 1,9
|
| 1,5
|
| 1,2
|
| 19,3
| |
|
| 0,4
|
| 1,5
|
| 1,2
|
| 0,8
|
| 0,8
|
| 0,8
|
| 0,8
|
| 0,8
|
| 2,7
|
| 4,3
|
| 0,8
|
| 0,8
|
| 15,5
| |
|
| 2,7
|
| 0,4
|
| 1,2
|
| 0,0
|
| 0,0
|
| 0,0
|
| 0,8
|
| 2,0
|
| 1,6
|
| 0,8
|
| 2,0
|
| 0,4
|
| 11,7
| |
|
| 0,4
|
| 0,8
|
| 0,0
|
| 0,0
|
| 0,0
|
| 0,0
|
| 0,0
|
| 0,8
|
| 3,9
|
| 3,9
|
| 2,4
|
| 2,0
|
| 14,1
| |
|
| 3,6
|
| 3,2
|
| 2,8
|
| 2,0
|
| 0,8
|
| 0,8
|
| 0,4
|
| 3,2
|
| 4,0
|
| 9,3
|
| 4,8
|
| 6,1
|
| 41,2
| | Средние за 9 лет
| 8,22
| 3,17
| 7,33
| 2,82
| 6,22
| 2,40
| 4,89
| 1,88
| 3,78
| 1,46
| 3,56
| 1,37
| 3,44
| 1,33
| 7,11
| 2,74
| 13,78
| 5,31
| 14,67
| 5,65
| 12,56
| 4,84
| 10,67
| 4,11
| 96,22
| 37,06
| Таблица 20

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Хронометражно-табличная методика определения суточного расхода энергии студента Цель: познакомиться с хронометражно-табличным методом определения суточного расхода энергии...
ОЧАГОВЫЕ ТЕНИ В ЛЕГКОМ Очаговыми легочными инфильтратами проявляют себя различные по этиологии заболевания, в основе которых лежит бронхо-нодулярный процесс, который при рентгенологическом исследовании дает очагового характера тень, размерами не более 1 см в диаметре...
Примеры решения типовых задач. Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2
Пример 1.Степень диссоциации уксусной кислоты в 0,1 М растворе равна 1,32∙10-2. Найдите константу диссоциации кислоты и значение рК.
Решение. Подставим данные задачи в уравнение закона разбавления
К = a2См/(1 –a) =...
|
Сущность, виды и функции маркетинга персонала Перснал-маркетинг является новым понятием. В мировой практике маркетинга и управления персоналом он выделился в отдельное направление лишь в начале 90-х гг.XX века...
Разработка товарной и ценовой стратегии фирмы на российском рынке хлебопродуктов В начале 1994 г. английская фирма МОНО совместно с бельгийской ПЮРАТОС приняла решение о начале совместного проекта на российском рынке. Эти фирмы ведут деятельность в сопредельных сферах производства хлебопродуктов.
МОНО – крупнейший в Великобритании...
ОПРЕДЕЛЕНИЕ ЦЕНТРА ТЯЖЕСТИ ПЛОСКОЙ ФИГУРЫ Сила, с которой тело притягивается к Земле, называется силой тяжести...
|
|

 ;
;  ;
; 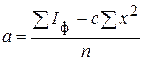 ;
;  ;
;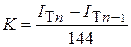 .
.
 V. Построение типовой и групповых кривых годовой динамики заболеваемости, т.е. графическое изображение сезонных колебаний. Для этих целей используют линейные (рис. 18, 19) и радиально-круговые диаграммы (рис. 20, 21).
V. Построение типовой и групповых кривых годовой динамики заболеваемости, т.е. графическое изображение сезонных колебаний. Для этих целей используют линейные (рис. 18, 19) и радиально-круговые диаграммы (рис. 20, 21).


