ПРИЛОЖЕНИЕ Л. Рассеяние фотона на свободном электроне
Рассмотрим столкновение фотона со свободным электроном в рамках релятивистской механики. Обозначим через Eγ и p γ энергию и импульс фотона до рассеяния, а через Eγ ’ и p γ ’ – после рассеяния. Для электрона полная энергия и импульс до рассеяния будут соответственно E 0 = mec 2 и 0 (электрон до рассеяния покоился), а после рассеяния Ee и p e. Тогда законы сохранения энергии и импульса дают
Отсюда
Для каждой частицы величина
есть инвариант, причем для фотона этот инвариант равен нулю. С учетом этого
Подставляя это в (Л.1), получаем
или
Обозначив угол рассеяния фотона (угол между векторами p γ и p γ ’) через θ;, перепишем (Л.2) в виде
Выразим теперь импульсы падающего и рассеянного фотона через соответствующие длины волн:
Из (Л.4) следует независимость комптоновского смещения
– одна из важнейших атомных постоянных. Она называется комптоновской длины волны электрона и представляет собой изменение длины волны фотона при его рассеянии на угол θ; = π/2. Ее связь с другими постоянными: При рассеянии фотона на электроне последний получает энергию отдачи
Переписав (Л.3) в виде
и выразив из (Л.6) Eγ ’, найдем, что
Как следует из (Л.7), кинетическая энергия комптоновского электрона минимальна (равна нулю) при рассеянии фотона вперед (θ; = 0) и максимальна при обратном рассеянии (θ; = π). В последнем случае
где x = 2 Eγ / E 0. Таким образом, при увеличении энергии фотона максимальная энергия комптоновских электронов стремится к величине Eγ.
|

 .
.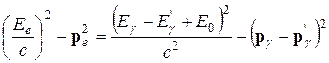 . (Л.1)
. (Л.1)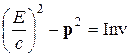
 .
. ,
, . (Л.2)
. (Л.2) . (Л.3)
. (Л.3)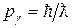 и
и 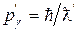 . Тогда
. Тогда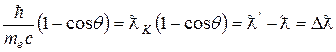 . (Л.4)
. (Л.4)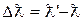 от рассеивающего вещества и первоначальной длины волны. Постоянная
от рассеивающего вещества и первоначальной длины волны. Постоянная (Л.5)
(Л.5)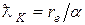 , где α; = e 2/ ħc – постоянная тонкой структуры, re = e 2/ mec 2 – классический радиус электрона. Существуют также комптоновские длины волн протона, нейтрона и других элементарных частиц. Все они определяются формулой (Л.5), если вместо массы электрона в нее подставить массу соответствующей частицы.
, где α; = e 2/ ħc – постоянная тонкой структуры, re = e 2/ mec 2 – классический радиус электрона. Существуют также комптоновские длины волн протона, нейтрона и других элементарных частиц. Все они определяются формулой (Л.5), если вместо массы электрона в нее подставить массу соответствующей частицы. . (Л.6)
. (Л.6)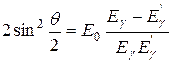
 . (Л.7)
. (Л.7)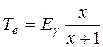 , (Л.8)
, (Л.8)


