Моменты случайных величин. Асимметрия и эксцесс.
Моментом n-го порядка Х по отн-ию к знач-ию а Mn(a)=M(X-a)n, а=0-начальный момент ύn ф=Ь(Ч)-центральный μn Для ДСВ: ύn= Для НСВ: ύn= Можно показать что справедлива формула: μn= μ2=ύ2-ύ12 μ3=ύ3-3ύ2 ύ1+2ύ12 μ4=ύ4-4ύ1 ύ3+6ύ12 ύ2-3ύ14 На практике при изуч. распределения отличного от норм. необх. колич. оценить эти различия для этого вводятся вспомог.числ. хар-ки ассиметрия и эксцесс.Центр. момент 3-го порядка μ3 характ-ет отклонение распределения СВХ от симметрии относит. мат.ожид.За меру этого отклонения берут число: α = μ3/σ3(х)-коэф.ассиметрии. Ассиметрия всех распред-ий графики которых симметр. относит.прямой х=а=М(х) равна 0. Центр.момент 4-го порядка μ4 служит для хар-ки крутости распред-ия СВ Х по сравнению с крутостью распред-ия НСВ с мат.ожид.и дисп. такими же как и у Х.За меру этой крутости берут число: χ = [ μ4/σ4(х) ] -3
Рис.1Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у). Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности) непрерывной двумерной случайной величины называ-ется смешанная частная производная 2-го порядка от функции распределения: 2) (cледует из определения двумерной плотности вероятно-сти). Аналогично определяется условная плотность вероятности Y при Х = х
|

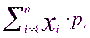
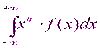
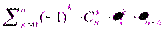
 F (х, у) = p (X < x, Y < y). (8.1)
F (х, у) = p (X < x, Y < y). (8.1)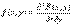 . (8.2) Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δ х и Δ у к площади этого прямоугольника при
. (8.2) Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δ х и Δ у к площади этого прямоугольника при 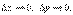 Свойства двумерной плотности вероятности.1) f (x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).
Свойства двумерной плотности вероятности.1) f (x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен). 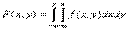
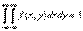 3) (поскольку это вероятность того, что точка попадет на плос-кость О ху, то есть достоверного события). Условной плотностью φ(х / у) распределения составляющих Х при данном значении Y = у называется
3) (поскольку это вероятность того, что точка попадет на плос-кость О ху, то есть достоверного события). Условной плотностью φ(х / у) распределения составляющих Х при данном значении Y = у называется 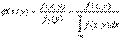 .
. .
.


