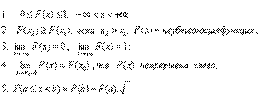Когда требуется спрогнозировать ожидаемую очередь и разумно сбалансировать число и производительность точек обслуживания и время ожидания в очереди. Пуассоновским называют закон распределения дискретной случайной величины Х числа появления некоторого события в n-независимых опытах если вероятность того, что событие появится ровно m раз определяется по формуле.
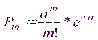 a=np
a=np
n-число проведенных опытов
р-вероятность появления события в каждом опыте
В теории массового обслуживания параметр пуассоновского распределения определяется по формуле
а=λt, где λ - интенсивность потока сообщений t-время
Необходимо отметить, что пуассоновское распределение является предельным случаем биномиального, когда испытаний стремится к бесконечности, а вероятность появления события в каждом опыте стремится к 0.  Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.
Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.
19.Геометрическое и гипергеометрическое распределения и их характеристики (вывод формулы). 1. Геометрическое распределение. Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (О < р < 1) и, следовательно, вероятность его не появления q = 1 - р. Испытания заканчиваются, как только появится событие А (т.е. количество испытаний неограниченно). Таким образом, если событие А появилось в k-м испытании, то в предшествующих k— 1 испытаниях оно не появлялось. Обозначим через X дискретную случайную величину - число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями Х являются натуральные числа: 1, 2, 3… Пусть в первых k— 1 испытаниях событие А не наступило, а в k-м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий, 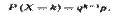
Полагая k= 1, 2,... в формуле, получим геометрическую прогрессию с первым членом р и знаменателем q 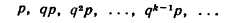
 ^ По этой причине распределение называют геометрическим. Легко убедиться, что ряд сходится и сумма его равна единице. Действительно, сумма ряда есть сумма членов бесконечной геометрической прогрессии со знаменателем меньшим единицы, тогда сумма его:
^ По этой причине распределение называют геометрическим. Легко убедиться, что ряд сходится и сумма его равна единице. Действительно, сумма ряда есть сумма членов бесконечной геометрической прогрессии со знаменателем меньшим единицы, тогда сумма его: 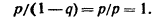
Замечание: если количество испытаний ограничено каким- либо натуральным числом k, то последнее значение вероятности в ряде распределения будет равно q k -1, означающее, что в предыдущих k -1 испытаниях событие А не появилось. 2.Гипергеометрическое распределение. Многие задачи комбинаторики могут быть сведены к следующей модели. В генеральной совокупности из n элементов имеется 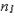 элементов красного цвета и
элементов красного цвета и 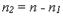 черного. Случайным образом выбирается группа из r элементов. Найдем вероятность
черного. Случайным образом выбирается группа из r элементов. Найдем вероятность  того, что так выбранная группа будет содержать ровно k красных элементов. Здесь k может быть любым целым числом между нулем и наименьшим из чисел
того, что так выбранная группа будет содержать ровно k красных элементов. Здесь k может быть любым целым числом между нулем и наименьшим из чисел  и r.
и r.
Для того, чтобы найти 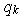 , заметим, что выбранная группа состоит из k красных и r-k черных элементов. Красные элементы могут быть выбраны
, заметим, что выбранная группа состоит из k красных и r-k черных элементов. Красные элементы могут быть выбраны 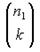 различными способами, а черные
различными способами, а черные 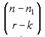 способами. Так как любой выбор красных элементов может комбинироваться с любым выбором черных, имеем
способами. Так как любой выбор красных элементов может комбинироваться с любым выбором черных, имеем  … (1).Определенный таким образом набор вероятностей называется гипергеометрическим распределением. Используя формулу
… (1).Определенный таким образом набор вероятностей называется гипергеометрическим распределением. Используя формулу 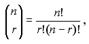 можно переписать (1) в виде
можно переписать (1) в виде
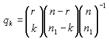 … (2).
… (2).
Замечание. Вероятности 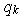 определены только для k, не превосходящим r или
определены только для k, не превосходящим r или  , но, так как при b>a
, но, так как при b>a 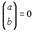 , из формулы (1) и (2) следует, что
, из формулы (1) и (2) следует, что 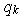 = 0, если либо k>;
= 0, если либо k>;  , либо k>r. Следовательно, определения (1) и (2) могут использоваться для всех при условии, что соотношение
, либо k>r. Следовательно, определения (1) и (2) могут использоваться для всех при условии, что соотношение 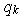 = 0 интерпретируется как невозможность такого выбора.
= 0 интерпретируется как невозможность такого выбора.
Примеры.
Проверка качества. При контроле качества продукции выборочной проверке подвергается партия из n изделий. Дефектные изделия в партии играют роль красных элементов. Их число  , конечно, не известно. Производится выборка объема r и определяется число k дефектных изделий в ней. Тогда формула (1) позволяет нам сделать выводы относительно истинного значения
, конечно, не известно. Производится выборка объема r и определяется число k дефектных изделий в ней. Тогда формула (1) позволяет нам сделать выводы относительно истинного значения  .
.
20.Функция распределения непрерывной случайной величины и ее свойства. График функции распределения НСВ. Функцией распределения называют функцию Р (х), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение, меньшее х, т. е.
F(х)=Р(Х<х).Часто вместотермина «функция распределения»используюттермин «интегральный закон распределения». свойства:
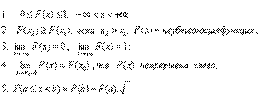

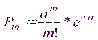 a=np
a=np Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.
Пуассоновское распределение является единичным распределением для которого такие характеристики как мат. Ожидание и дисперсия совпадают и они равны параметру этого закона распределения а.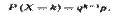
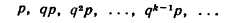
 ^ По этой причине распределение называют геометрическим. Легко убедиться, что ряд сходится и сумма его равна единице. Действительно, сумма ряда есть сумма членов бесконечной геометрической прогрессии со знаменателем меньшим единицы, тогда сумма его:
^ По этой причине распределение называют геометрическим. Легко убедиться, что ряд сходится и сумма его равна единице. Действительно, сумма ряда есть сумма членов бесконечной геометрической прогрессии со знаменателем меньшим единицы, тогда сумма его: 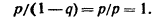
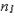 элементов красного цвета и
элементов красного цвета и 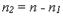 черного. Случайным образом выбирается группа из r элементов. Найдем вероятность
черного. Случайным образом выбирается группа из r элементов. Найдем вероятность  того, что так выбранная группа будет содержать ровно k красных элементов. Здесь k может быть любым целым числом между нулем и наименьшим из чисел
того, что так выбранная группа будет содержать ровно k красных элементов. Здесь k может быть любым целым числом между нулем и наименьшим из чисел  и r.
и r.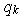 , заметим, что выбранная группа состоит из k красных и r-k черных элементов. Красные элементы могут быть выбраны
, заметим, что выбранная группа состоит из k красных и r-k черных элементов. Красные элементы могут быть выбраны 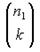 различными способами, а черные
различными способами, а черные 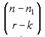 способами. Так как любой выбор красных элементов может комбинироваться с любым выбором черных, имеем
способами. Так как любой выбор красных элементов может комбинироваться с любым выбором черных, имеем  … (1).Определенный таким образом набор вероятностей называется гипергеометрическим распределением. Используя формулу
… (1).Определенный таким образом набор вероятностей называется гипергеометрическим распределением. Используя формулу 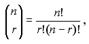 можно переписать (1) в виде
можно переписать (1) в виде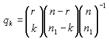 … (2).
… (2). , но, так как при b>a
, но, так как при b>a 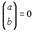 , из формулы (1) и (2) следует, что
, из формулы (1) и (2) следует, что