Равномерный закон распределения и его числовые характеристики.
Непр. случ. велич.х распред. равномерно на отрезк [а;b], если её плотность вероятности р(х) постоянна на этом отрезке и =0 вне его: 1/ (b-a), а< =х<=b Р(х)= { О, х<а, х>b Функция распред. случайн. величины, расп- ред-ой по равномерн. закону, имеет вид: O, x<=a F(x)= { (x-a)/(b-a), a<x<=b 1, x>b График р(х) иF(х)на рис Мат. ожидание и дисперсия равн. случ. величины: МХ=(а+b)/2; DХ=(b-а)(b-a)/ 12 24.Показательный закон распределения и его числовые характеристики. Непрерывная СВ Х имеет показ. (экспоненциальное) распределение с параметром λ >0, если ее плотность распред-я имеет вид: Ф-ция распределения СВ, распределенной по показ. з-ну: Показательному распределению обычно подчиняется величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств, другими словами – величина промежутка времени между появлениями двух послед-х редких событий. Вероятность попадания случайной величины Х на интервал (α;β)
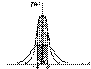
Влияние параметров а и σ на вид нормальной кривой.Нормальное распределение явл. одним из наиболее часто встречающихся. Играет большую роль в тер. вер., поскольку явл. Предельным законом, к к-ому приближаются все др. законы распределения.Док-но, что если знач. СВ возникают в результате большого числа независимых воздействий, ни одно из к-ых не превалирует над остальными, то результат этих воздействий явл. СВ, распределенной по нормальному закону почти всегда.По нормальному закону распределены:случайные ошибки измерения,лин. размеры деталей при массовом пр-ве,биометрические показатели лиц определенного возраста,отклонения в результате хим., спектральных и других анализах. Говорят, что непрерывная СВ Х имеет нормальное распределение с параметрами а и σ, если ее плотность распределения имеет вид -(x- a)2/2σ2 f(x)=(1/σ√2π) e Определение корректно, т.к.: -∞∫+∞f(x)dx=1 ^ M(X)= -∞∫+∞xf(x)dx=a σ (X)= -∞∫+∞(x-M(X))2f(x)=σ2 Для геометрической интерпретации параметров а и σ исследуют поведение ф-ии -(x-a)2/2σ2 f(x)=(1/σ√2π) e график к-ой наз. нормальной кривой. График симметр.относит. а При изменении параметра а форма кривой не меняется, а ее график сдвигается влево или вправо. При изменении параметра σ меняется форма нормальной кривой: с увеличением параметра σ кривая должна приближаться к 0Х и растягиваться вдоль этой оси, а с уменьшением σ кривая стягивается к прямой х=а. = ормированное нормальное распределение имеет параметры Плотность распределения вероятностей нормированного нормального распределения записывается в виде: На рисунке наглядно показано, что если две случайные величины нормально распределены и а = 0, то вероятность принять значение, принадлежащее интервалу (-d,d),больше у той величины, которая имеет меньшее значение d. Этот факт полностью соответствует вероятностному смыслу параметра s.
27. Правило трех сигм и его значение для праклики При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины D:
|


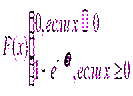
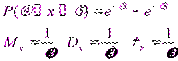
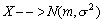 в заданный интервал
в заданный интервал 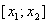 с помощью функции Лапласа, сначала с.в. Х нормализуется (см. 4.24), а затем используется следующая формула:
с помощью функции Лапласа, сначала с.в. Х нормализуется (см. 4.24), а затем используется следующая формула: 

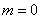 и
и 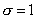 . Это распределение получается, если пронормировать нормально распределенную величину X по формуле:
. Это распределение получается, если пронормировать нормально распределенную величину X по формуле:  (4.24)
(4.24) ^ Вероятность заданного отклонения равна
^ Вероятность заданного отклонения равна 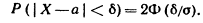
 Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа:
Если принять D = 3s, то получаем с использованием таблиц значений функции Лапласа: 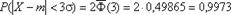 Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее. На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую чем утроенное среднее. На практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение.


