Следует закон больших чисел
n limP(|1/n сумма (Xi)- a| <=e)=1 n-& i=1 Смысл закона закл. в том, что средние значения случайных величин стремятся к их мат. ожиданию при n- & по вероятн. Отклонение средн. значений от мат.ожидания стан-ся сколь угодно малым с вероятностью, близкой к 1, если n достаточно велико или вероятность любого откл. средн. знач. от а сколь угодно мала с ростом n. (e – это эпсилон.)
Теорема Бернулли: Если вер-ть наст-я соб-я А в каж-м из n повторных нез-х испыт-й пост-на, то при неогран-м увел-ии числа n исп-й отн-я частота Т-ма Б-ли явл-ся теор-ким обосн-ем для стат-го опр-я вер-ти. Неравенство Бернулли: Пусть
Пусть производится последовательность независимых испытаний, в результате каждого из которых может наступить или не наступить событие А, причем вероятность наступления этого события одна и та же при каждом испытании и равна р. Если событие А фактически произошло m раз в n испытаниях, то отношение m/n называют, как мы знаем, частотой появления события А. Частота есть случайная величина, причем вероятность того, что частота принимает значение m/n, выражается по формуле Бернулли (13):
иными словами, при неограниченном увеличении числа n опытов частота m/n события А сходится по вероятности к Р(А). (Доказательство) Мы говорили (см. § 1, п. 1), что при большом числе испытаний частота Р*(А)=m/n события А обладает свойством устойчивости. Это обстоятельство находит свое объяснение в законе больших чисел Бернулли.
|

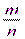 наст-я соб-я А стрем-ся по вер-ти к числу p, т.е. для
наст-я соб-я А стрем-ся по вер-ти к числу p, т.е. для 
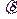 >0
>0 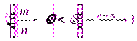
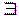 n исп-й Бернулли с вер-ю успеха p, q=1-p и m – число успехов. Тогда для
n исп-й Бернулли с вер-ю успеха p, q=1-p и m – число успехов. Тогда для 
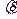 >0
>0





