Интервальный вариационный ряд
Характеризует распределение единиц совокупности по количественному признаку, величина ко- торого может принимать в определенных пределах любые значения, отличающиеся друг от друга на сколь угодно малую величину. После определения исследуемого признака, необходимо решить вопрос о количестве групп (ин- тервалов), на которые надо разбить выборку.Выборочная дисперсия является смещённой оценкой теоретической дисперсии, а исправленная выборочная дисперсия несмещённая:
Интервальные оценки параметров. Доверительный интервал Интервальной оценкой называют оценку, которая определяется двумя числами — концами интервала, который с определенной вероятностью накрывает неизвестный параметр генеральной совокупности. Интервал, содержащий оцениваемый параметр генеральной совокупности, называют доверительным интервалом. Для его определения вычисляется предельная ошибка выборки, позволяющая установить предельные границы, в которых с заданной вероятностью (надежностью) должен находиться параметр генеральной совокупности.Предельная ошибка выборки равна t-кратному числу средних ошибок выборки. Коэффициент t позволяет установить, насколько надежно высказывание о том, что заданный интервал содержит параметр генеральной совокупности. Если выбирается коэффициент таким, что высказывание в 95% случаев окажется правильным и только в 5% — неправильным, то говорится, что: со статистической надежностью в 95% доверительный интервал выборочной статистики содержит параметр генеральной совокупности. Статистической надежности в 95% соответствует доверительная вероятность — 0,95. В 5% случаев утверждение «параметр принадлежит доверительному интервалу» будет неверным, т. е. 5% задает уровень значимости () или 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% (α < 0,05). Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания. С помощью доверительного интервала можно оценить не только генеральную среднюю, но и другие неизвестные параметры генеральной совокупности. 43.Статистическая проверка гипотез. Критерий проверки, ошибки первого и второго рода, критическая область. ^ СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ - система приемов в математической статистике, предназначенная для проверки соответствия опытных данных проверяемой гипотезе. К проблеме статистической проверки гипотез приводит большое число связанных с экспериментом вопросов, возникающих в приложениях, напр. сравнение урожайности сортов каких-либо сельскохозяйственных культур, эффективности лекарственных препаратов и др. Правило, по которому принимается или отклоняется данная гипотеза, называют статистическим критерием.При проведении экономико-статистических исследований в первую очередь приходится решать задачи статистической проверки гипотез о: Правосторонняя критическая область определяется интервалом 44.Критерий согласия Пирсона о законе распределения случайной величины. Критерий Пирсона, или критерий χ2 — наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая требует статистической проверки.Обозначим через X исследуемую случайную величину. Пусть требуется проверить гипотезу H 0 о том, что эта случайная величина подчиняется закону распределения F (x). Для проверки гипотезы произведём выборку, состоящую из n независимых наблюдений над случайной величиной X. По выборке можно построить эмпирическое распределение F * (x) исследуемой случайной величины. Сравнение эмпирического F * (x) и теоретического распределений производится с помощью специально подобранной случайной величины — критерия согласия. Одним из таких критериев и является критерий Пирсона. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной. Вопросы по курсу «Теория вероятностей и математическая статистика»
1. 2. 3. 4. 5. 6. 7.
|

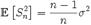 ,и
,и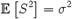 .
.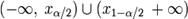 , где
, где  находят из условий
находят из условий 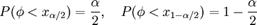 . Левосторонняя критическая область определяется интервалом
. Левосторонняя критическая область определяется интервалом 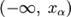 , где x α находят из условия P (φ < x α) = α.
, где x α находят из условия P (φ < x α) = α. , где x 1 − α находят из условия P (φ < x 1 − α) = 1 − α.
, где x 1 − α находят из условия P (φ < x 1 − α) = 1 − α.


