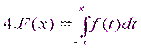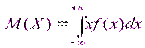Плотность распределения вероятностей непрерывной случайной величины и ее свойства.
Судить о хар-ре распр-ия в небольшой окрестности точек числ. оси позвол-т плотность распределения вер-ей. Рассм-м НСВ Х с интегр.непр-но диф-ой ф-ией распр-ия F(x). Вер-ть попад-ия этой вел-ны в интервал (х,х+∆х) равна Р(х<X<x+∆x)=F(x+∆x)-F(x). Вер-сть, к-рая находится на ед-цу длины рассмарт-го интервала: (Р(х<X<x+∆x))/∆x=(F(x+∆x)-F(x))/∆x. Если мы перейдем к пределам, то получим вер-ть, кот. прих-ся на изолиров-ую точку Х: f(x)=F’(x). График ПР вер-тей – кривой распр-ия CВ Х. Cв-ва ПР: 1.f(x)≥0 для люб.x – cв-во неотриц-ти.
3. Cв-во нормировки.
НСВ- св которая может принять любое значение из некоторого конечного или бесконечного интнрвала.
Геом.смысл: абсцесса центра тяжести криволин. трапеции огранич. графиком кр. распред-ия полигоном распред для ДСВ и Ох. D(X)=M(X-M(X))2 σ (Х)= D(X)1/2 D(X)= M(X)2-M2(X)
|
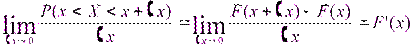Пл-тью распр-ия вер-тей (диф.фун-ей распр-ия) наз-ся первая производная интегр. ф-ции распр-ния F(x):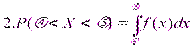
-
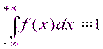