Рассмотрим случай многократного повторения одного и того же испытания или
случайного эксперимента. Результат каждого испытания будем считать не зависящим
от того, какой результат наступил в предыдущих испытаниях. В качестве результатов
или элементарных исходов каждого отдельного испытания будем различать лишь две
возможности:
1) появление некоторого события А;
2) появление события 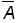 , (события, являющегося дополнением А)
, (события, являющегося дополнением А)
Пусть вероятность P(A) появления события А постоянна и равна p (0<.p<1).
Вероятность P(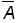 ) события
) события 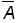 обозначим через q: P(
обозначим через q: P(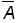 ) = 1- p=q.
) = 1- p=q.
. Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют "независимыми относительно события А"(Событие А имеет одну и ту же вероятность) "Сложное событие"- совмещение нескольких отдельных событий, которые называют "простыми". Пусть производится n независимых испытаний, в каждом из которых событие А может появиться либо не появиться. Теорема. Если производится n независимых опытов в каждом из которых событие А появляется с одинаковой вероятностью р, причем то тогда вероятность того, что событие А появится ровно m раз определяется по формуле. 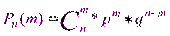
формула Бернули применяется в тех случаях, когда число опытов невелико, а вероятности появления достаточно велики.
^ 9Наивероятнейшее число появления события (вывод неравенства). Вероятность можно рассматривать как функцию целочисленного аргумента m.Существует такое значение аргумента 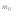 , при котором эта функция принимает наибольшее значение
, при котором эта функция принимает наибольшее значение 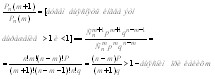
np-mp>mq+q m(q+p)<np-q, где q+p=1 m<np-q Вывод при таких m 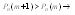 при таких m функция возростает. И наоборот при m>np-q
при таких m функция возростает. И наоборот при m>np-q
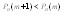 , то есть при таких m функция убывает, то есть действителен один
, то есть при таких m функция убывает, то есть действителен один 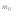 при котором функция достигает max значенияПо смыслу
при котором функция достигает max значенияПо смыслу 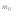 должны выполняться два неравенства
должны выполняться два неравенства 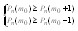
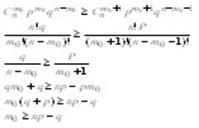
Распишем 2-е неравенство
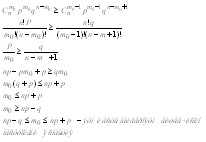
(9) (продолжение)Наивероятнейшее число 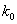 появления события при
появления события при 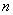 независимых испытаниях:
независимых испытаниях:
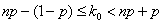 ,
, 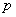 - вероятность появления события при одном испытании.
- вероятность появления события при одном испытании.

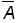 , (события, являющегося дополнением А)
, (события, являющегося дополнением А)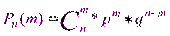
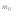 , при котором эта функция принимает наибольшее значение
, при котором эта функция принимает наибольшее значение 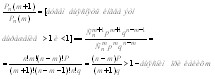
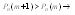 при таких m функция возростает. И наоборот при m>np-q
при таких m функция возростает. И наоборот при m>np-q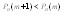 , то есть при таких m функция убывает, то есть действителен один
, то есть при таких m функция убывает, то есть действителен один 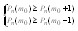
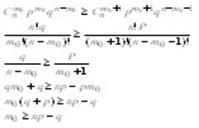
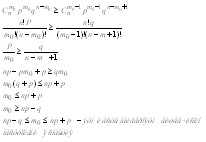
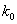 появления события при
появления события при 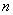 независимых испытаниях:
независимых испытаниях: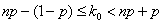 ,
, 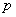 - вероятность появления события при одном испытании.
- вероятность появления события при одном испытании.


