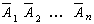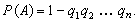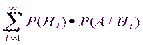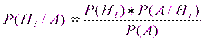Зависимые и независимые события. Условная вероятность. Теоремы умножения вероятностей.
1) Условная вероятность события А при условии В равна Р(А/B)=P(A*B)/P(B), Р(В)>0. 2) Событие А не зависит от события В, если Р(А/B)=P(A). Независимость событий взаимна, т.е. если событие А не зависит от В, то событие В не зависит от А. В самом деле при Р(А)>0 имеем Р(B/A)=P(A*B)/P(A)=P(A/B)*P(B)/P(A)=P(A)*P(B)/P(A)=P(B). Вытекает следующая формула умножения вероятностей: Р(А*В)=Р(А)*Р(В/A). Для независимых событий вероятность произведения событий равна произведению их вероятностей: Р(А*В)=Р(А)*Р(В). 3) События А1,А2,…,Аn образуют полную группу событий, если они попарно несовместны и вместе образуют достоверное событие, т.е. Аi*Aj=0, i не=j, U по i от 1 до n Аi=омега. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ)=Р(А)*Ра(В). В частности для независимых событий Р(АВ)=Р(А)*Р(В), т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Ч а с т н ы й с л у ч а й. Если события А1, А2,..., Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий (A) = l — q n. (**) Док-во Обозначим через А событие, состоящее в появлении хотя бы одного из событий А1,А2,...,An. События А и
Отсюда, пользуясь теоремой умножения, получим
или
Вероятность появления хотя бы одного из событий А1, А2,…,Аn независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий, т.е.
^ 7.Формула полной вероятности и формула Байеса. Формула Бейса Пусть имеется полная группа попарнонесовместных гипотез Н1,Н2…Нn с известными вероятностями появления. В результате проведения опыта появилось некоторое события А, требуется переоценить вероятности гипотез при условии, что событие А произошло
|

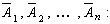 Р (A) = 1 — q 1 q 2... q n.(*)
Р (A) = 1 — q 1 q 2... q n.(*)