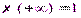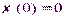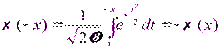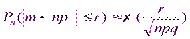Интегральная.Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что в этих испытаниях событие А появится число раз, заключенное в границах [a;b], может быть посчитана по формуле:
Функция нечетная, возрастающая X>4, Ф(х)=1 Следствие из интегральной теоремы Муавра-Лапласа. Если число повторных независимых испытаний достаточно велико, вероятность появления события А в каждом испытании постоянно и отлично от нуля и единицы, то вероятность того, что число появлений события А отклонится от произведения np не больше, чем на некоторое положительное число r по модулю, может быть посчитано по формуле
|
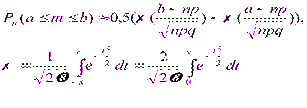Свойства функции Лапласа:
