Дисперсия дискретной случайной величины и ее свойства. Среднее квадратичное отклонение. Размерность дисперсии и среднеквадратичного отклонения.
^ Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: Дисперсию удобно вычислять по формуле Свойства дисперсии: ^ Средним квадратическим отклонением случайной величины называют квадратный корень из ее дисперсии:
Пусть проводится n независимых испытаний. В результате каждого из которых возможны 2 исхода: А – успех с вероятностью p, или Дискретная случайная величина X, которая может принимать только целые неотрицательные значения с вероятностями P (X=m)= Мат.ожидание Дисперсия
D(x)=
|
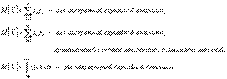
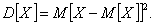
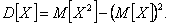
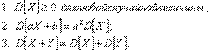
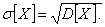
- неуспех с вероятностью q = 1-p. Тогда вероятность числа m успех 
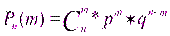
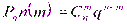, где p>0, q>0, m 
0,n называется распределенной по биноминальному закону с параметром p.
M(X)= np
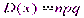
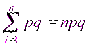
- среднее квадратическое отклонение
