Мы приведем без доказательства вариант ЦПТ для независимых одинаково распределенных слагаемых.
Центральная Предельная Теорема 1 Пусть  -- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим
-- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим 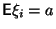 и
и 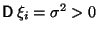 . Тогда
. Тогда 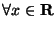
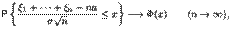
где 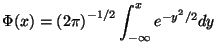 -- функция распределения стандартного нормального закона.
-- функция распределения стандартного нормального закона.
37.Предмет и задачи математической статистики. Генеральная и выборочная совокупности. Способы отбора. Задачи математической статистики Математическая статистика, раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических выводов. При этом статистическими данными называются сведения о числе объектов в какой-либо более или менее обширной совокупности, обладающих теми или иными признаками. Предмет и метод математической статистики. Статистическое описание совокупности объектов занимает промежуточное положение между индивидуальным описанием каждого из объектов совокупности, с одной стороны, и описанием совокупности по её общим свойствам, совсем не требующим её расчленения на отдельные объекты, — с другой. По сравнению с первым способом статистические данные всегда в большей или меньшей степени обезличены и имеют лишь ограниченную ценность в случаях, когда существенны именно индивидуальные данные (например, учитель, знакомясь с классом, получит лишь весьма предварительную ориентировку о положении дела из одной статистики числа выставленных его предшественником отличных, хороших, удовлетворительных и неудовлетворительных оценок). С другой стороны, по сравнению с данными о наблюдаемых извне суммарных свойствах совокупности статистические данные позволяют глубже проникнуть в существо дела. Метод исследования, опирающийся на рассмотрение статистических данных о тех или иных совокупностях объектов, называется статистическим. Статистический метод применяется в самых различных областях знания. Множество всех единиц совокупности, обладающих определенным признаком и подлежащих изучению, носит в статистике название генеральной совокупности. На практике по тем или иным причинам не всегда возможно или же нецелесообразно рассматривать всю генеральную совокупность. Тогда ограничиваются изучением лишь некоторой части ее, конечной целью которого является распространение полученных результатов на всю генеральную совокупность, т. е. применяют выборочный метод. Для этого из генеральной совокупности особым образом отбирается часть элементов, так называемая выборка, и результаты обработки выборочных данных (например, средние арифметические значения) обобщаются на всю совокупность.
38.Построение дискретного вариационного ряда. Эмпирическая функция распределения и ее свойства. Дискретный вариационный ряд характеризует распределение единиц совокупности по дискретному признаку, принимающему только целые значения. Для его построения следует перечислить все встречающиеся варианты значений признака и подсчитать частоту повторения. При графическом изображении дискретных вариационных рядов используется полигон распределения, или полигон частот. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении абсцисс и ординат точки соединяются прямыми линиями, в результате чего получают ломаную линию.Эмпирической функцией распределения (функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения x относительную частоту события X<x. Та-ким образом, по определению F*(x)= Nx/N, где Nx–число вариант, меньших x, n – объем выборки. Свойства:1)Значения эмпирической функции принадлежат отрезку [0,1].
2)неубывающая функция.
3)Если x – наименьшая варианта, то F*(x)=0 при x<=Xk,
если x– наибольшая варианта, тоF*(x)=1 при x>Xk.
Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности.
39.Построение интервального вариационного ряда. Гистограмма частот и относительных частот. Для построения интервального вариационного ряда, характеризующего распределение банков по объему кредитных вложений, необходимо вычислить величину и границы интервалов ряда
При построении ряда с равными интервалами величина интервала h определяется по формуле 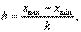 (1) где xmax, xmin - наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.Число групп k задается в условии задания или рассчитывается по формуле Г. Стерджесса Полигоном частот называется ломаная линия, вершинами которой служат точки с координатами (хi;ni), i=1…k.Для группировки выборки строят гистограмму частот, т.е. ступенчатую фигуру, состоящую из прямоугольников,площадь прямоугольника равна частоте ñi*.Площадь гистограммы равна объему выборки.Высота прямоугольников равна ñ*i / n. Для изображения интервального вариационного ряда используется гистограмма. На оси абсцисс
(1) где xmax, xmin - наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.Число групп k задается в условии задания или рассчитывается по формуле Г. Стерджесса Полигоном частот называется ломаная линия, вершинами которой служат точки с координатами (хi;ni), i=1…k.Для группировки выборки строят гистограмму частот, т.е. ступенчатую фигуру, состоящую из прямоугольников,площадь прямоугольника равна частоте ñi*.Площадь гистограммы равна объему выборки.Высота прямоугольников равна ñ*i / n. Для изображения интервального вариационного ряда используется гистограмма. На оси абсцисс
откладываются величины интервалов, а частоты изображаются прямоугольниками, построенными
на соответствующих интервалах. Высота столбцов гистограммы должна быть пропорциональна частотам.

 -- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим
-- последовательность независимых одинаково распределенных с.в. с конечной дисперсией. Обозначим 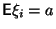 и
и 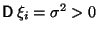 . Тогда
. Тогда 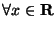
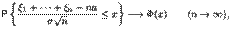
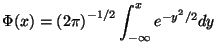 -- функция распределения стандартного нормального закона.
-- функция распределения стандартного нормального закона.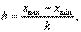 (1) где xmax, xmin - наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.Число групп k задается в условии задания или рассчитывается по формуле Г. Стерджесса Полигоном частот называется ломаная линия, вершинами которой служат точки с координатами (хi;ni), i=1…k.Для группировки выборки строят гистограмму частот, т.е. ступенчатую фигуру, состоящую из прямоугольников,площадь прямоугольника равна частоте ñi*.Площадь гистограммы равна объему выборки.Высота прямоугольников равна ñ*i / n. Для изображения интервального вариационного ряда используется гистограмма. На оси абсцисс
(1) где xmax, xmin - наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.Число групп k задается в условии задания или рассчитывается по формуле Г. Стерджесса Полигоном частот называется ломаная линия, вершинами которой служат точки с координатами (хi;ni), i=1…k.Для группировки выборки строят гистограмму частот, т.е. ступенчатую фигуру, состоящую из прямоугольников,площадь прямоугольника равна частоте ñi*.Площадь гистограммы равна объему выборки.Высота прямоугольников равна ñ*i / n. Для изображения интервального вариационного ряда используется гистограмма. На оси абсцисс


