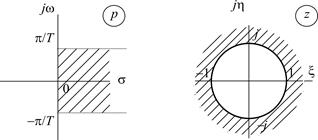
Отображение p-плоскости на z- плоскость
Используя взаимосвязь между комплексными переменными - характерных точек p -плоскости; - отрезков мнимой оси j w и всей оси j w p -плоскости; - коридоров в левой и правой p -полуплоскостях. 1. Начало координат p -плоскости – точка с координатами (s = 0; w = 0) отображается в точку z -плоскости с координатами (x = 0; h = 0); в полярных координатах (r = 1; j = 0), (рис. 1.11, табл.1.3):
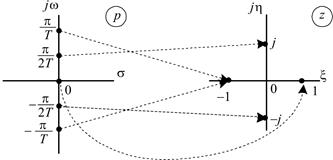
Рис. 1.11. Отображение точек p -плоскости на z -плоскость 2. Точка p -плоскости с координатами (s = –¥; w = 0) соответствует началу координат z -плоскости – точке с координатами (x = 0; h = 0):
3. Точка p- плоскости на оси частот j w с координатами (s = 0; w = p / 2 T) отображается в точку z -плоскости с координатами (x = 0; h = 1); в полярных координатах (r = 1; j = p/2), (рис. 1.11, табл.1.3):
4. Точка p- плоскости на оси j w с координатами (s = 0;
5. Две точки p- плоскости на оси j w с координатами (s = 0; w = ±p / 2 T) отображаются в одну точку z -плоскости с координатами (x = –1; h = 0); в полярных координатах (r = 1; j = ±p), (рис. 1.11, табл.1.3):
6. Отрезок оси частот j w p -плоскости
на z -плоскости отображается в окружность единичного радиуса (единичную окружность):
радиус-вектор совершает один полный оборот против часовой стрелки, начиная с точки Несложно показать, что при движении точки с начальными координатами (s = 0; w = p / T) вдоль оси j w вверх частотный интервал p < w ≤ (p + 2p k) Þ D Аналогично, при движении точки с начальными координатами (s = 0; w = –p / T) вдоль оси j w вниз частотный интервал –(p + 2p k) < w ≤ –p Þ D Таким образом, мнимая ось j w отображается в бесчисленное множество совпадающих единичных окружностей, вследствие чего возникает неоднозначность отображения точек p -плоскости на z -плоскость. Для их взаимно однозначного отображения ограниваются частотным диапазоном
в результате чего p -плоскость ограничивается «коридором» между двумя линиями, параллельными оси абсцисс
Рис. 1.12. Соответствие p - и z - плоскостей 7. Коридор в левой p- полуплоскости
на z- плоскости отображается в круг единичного радиуса (единичный круг) (рис. 1.13, табл.1.3
Рис. 1.13. Отображение «коридора» в левой p -полуплоскости на z -плоскость 8. Коридор в правой p- полуплоскости
на z- плоскости отображается в область вне единичного круга (рис. 1.14, табл.1.3):
Рис. 1.14. Отображение «коридора» в правой p -полуплоскости на z -плоскость
Таблица 1.3
|

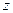 и
и 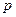 (1.24), рассмотрим отображение на z -плоскость:
(1.24), рассмотрим отображение на z -плоскость: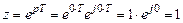 .
.
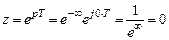 .
.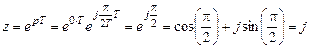 .
.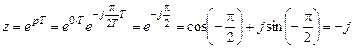 .
. .
.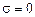 ;
; 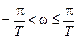
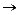
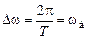
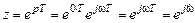 ;
;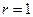 ;
; 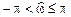
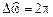 ;
;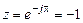 , т. е. угол j на z -плоскости ограничен областью главных значений.
, т. е. угол j на z -плоскости ограничен областью главных значений. отображается на z -плоскости в k совпадающих единичных окружностей
отображается на z -плоскости в k совпадающих единичных окружностей 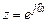 :
: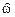 = 2p k, k = 1, 2, …
= 2p k, k = 1, 2, …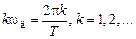 также отображается на z -плоскости в k совпадающих единичных окружностей
также отображается на z -плоскости в k совпадающих единичных окружностей  ®
® 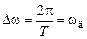 ,
,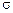 и пересекающими ось ординат j w в точках
и пересекающими ось ординат j w в точках 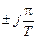 (рис. 1.12).
(рис. 1.12).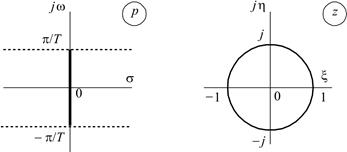
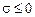 ;
; 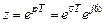 ;
;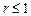 ;
; 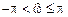 ®
® 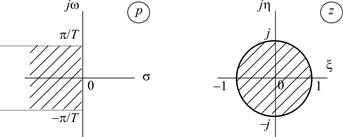
 ;
; 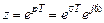 ;
;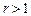 ;
;