Оценка устойчивости по передаточной функции
В п. 1.3.6 при описании ЛДС во временной области рассмотрен критерий, позволяющей оценить устойчивость ЛДС по ее импульсной характеристике. В z - области, где основной характеристикой ЛДС является передаточная функция (z -изображение ИХ), существует критерий, позволяющий оценить устойчивость ЛДС по передаточной функции, а именно: для того чтобы ЛДС была устойчива, необходимо и достаточно, чтобы все полюсы ее передаточной функции располагались внутри единичного круга комплексной z-плоскости
где На практике устойчивость рекурсивных ЛДС обычно оценивают по более удобному критерию (1.57) – положению полюсов на карте нулей и полюсов. 1.4.6. Нули и полюсы Звено 2-го порядка описывается передаточной функцией (1.47). Найдем комплексно-сопряженные полюсы в виде
где значения радиуса
Для вычисления нулей в общем случае следует умножить числитель и знаменатель ПФ (1.47) на
и найти корни уравнения числителя
которые могут быть вещественными или комплексно-сопряженными (в зависимости от знака дискриминанта):
Если нули – комплексно-сопряженные
их следует представить в показательной форме
где радиус
Если коэффициент
1.5. Описание линейных дискретных систем В разд. 1.3 рассматривалось описание ЛДС во временной области: импульсная характеристика и соотношение вход/выход в виде формулы свертки либо разностного уравнения. Здесь рассматривается их отображение в частотной области. Описание ЛДС в частотной области позволяет: - ввести фундаментальное для теории линейных систем понятие частотной характеристики; при проектировании большинства систем ЦОС именно к частотным характеристикам предъявляются и выдерживаются требования; - определять реакцию ЛДС в установившемся режиме не только на гармоническое воздействие, но и на любое воздействие, которое можно представить как линейную комбинацию гармонических воздействий. 1.5.1. Частотная характеристика. Соотношение вход/выход Основной характеристикой ЛДС в частотной областиявляется фурье-изображение импульсной характеристики
или для нормированных частоты и времени:
При известном фурье-изображении
где Определим ЧХ подобно тому, как это делается для линейных аналоговых систем, относительно которых известно, что гармоническое воздействие вызывает гармоническую реакцию той же частоты, но (в общем случае) другой амплитуды и начальной фазы. Рассмотрим реакцию ЛДС на дискретное комплексное гармоническое воздействие
с амплитудой и фазой соответственно
Для вычисления реакции воспользуемся формулой свертки (1.13)
откуда с учетом определения ЧХ (1.62)
На основании этого частотную характеристику можно представить как отношение
и определить следующим образом. Частотной характеристикой (ЧХ) Подчеркнем, что отношение (1.64) справедливо исключительно для гармонического воздействия и установившегося режима работы ЛДС. Поясним, смысл «установившегося режима». Теоретически, область изменения гармонического воздействия Комплексную функцию
Модуль частотной характеристики
а аргумент – фазочастотной характеристикой (ФЧХ) ЛДС
Поясним смысл АЧХ и ФЧХ, для чего перепишем выражение для реакции, подставив в него воздействие (1.63) и ЧХ (1.65):
откуда следует, что реакция на комплексный гармонический сигнал есть тоже комплексный гармонический сигнал той же частоты, что и воздействие, но с частотно-зависимыми амплитудой
и фазой
Сопоставив выражения для реакции (1.68) и воздействия (1.63), дадим определения АЧХ и ФЧХ. Амплитудно-частотной характеристикой ЛДС
Фазочастотной характеристикой ЛДС
|

 ,
,  1, 2,…,
1, 2,…,  , (1.57)
, (1.57) – k -й полюс ПФ (1.46).
– k -й полюс ПФ (1.46).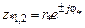 ,
,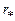 и угла
и угла 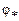 на комплексной z -плоскости выражаются через коэффициенты
на комплексной z -плоскости выражаются через коэффициенты  и
и  на основании соотношений (1.52) и (1.53) следующим образом:
на основании соотношений (1.52) и (1.53) следующим образом: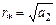 ; (1.58)
; (1.58)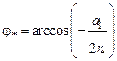 . (1.59)
. (1.59)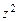
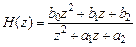
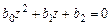 ,
,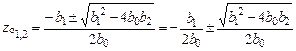 .
. ,
,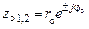 , (1.60)
, (1.60)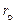 и угол
и угол 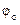 определяются из (1.31) и (1.32) соответственно:
определяются из (1.31) и (1.32) соответственно: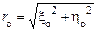 ;
;  .
.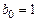 , то вычисление комплексно-сопряженных нулей можно упростить: не умножая числитель и знаменатель ПФ (1.47) на
, то вычисление комплексно-сопряженных нулей можно упростить: не умножая числитель и знаменатель ПФ (1.47) на 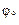 рассчитываются по формулам подобным (1.53)–(1.54), а именно:
рассчитываются по формулам подобным (1.53)–(1.54), а именно: ;
; 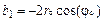 .
.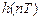 , которое определяется по формуле прямого преобразования Фурье
, которое определяется по формуле прямого преобразования Фурье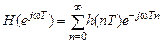 , (1.61)
, (1.61)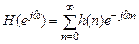 . (1.62)
. (1.62)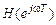 импульсная характеристика
импульсная характеристика  ,
,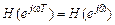 называют комплексной частотной характеристикой (КЧХ) или коротко частотной характеристикой (ЧХ); это математическое определение ЧХ.
называют комплексной частотной характеристикой (КЧХ) или коротко частотной характеристикой (ЧХ); это математическое определение ЧХ.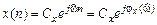 (1.63)
(1.63) ;
; 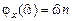 .
.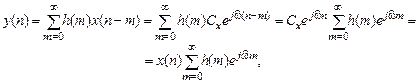
 .
.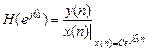 (1.64)
(1.64)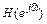 ЛДС называется частотная зависимость отношения реакции к дискретному гармоническому воздействию в установившемся режиме.
ЛДС называется частотная зависимость отношения реакции к дискретному гармоническому воздействию в установившемся режиме.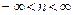 . Однако на практике имеют дело с условно гармоническим воздействием в области
. Однако на практике имеют дело с условно гармоническим воздействием в области  , где время
, где время 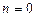 соответствуют началу воздействия. В течение времени
соответствуют началу воздействия. В течение времени 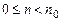 ЛДС работает в режиме переходныхколебаний. Спустя время
ЛДС работает в режиме переходныхколебаний. Спустя время  процесс устанавливается и реакция становится периодическим сигналом, поэтому в данном случае имеет смысл говорить о реакции как о гармоническом сигнале в установившемся режиме.
процесс устанавливается и реакция становится периодическим сигналом, поэтому в данном случае имеет смысл говорить о реакции как о гармоническом сигнале в установившемся режиме.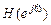 можно выразить через ее модуль и аргумент:
можно выразить через ее модуль и аргумент: . (1.65)
. (1.65)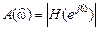 , (1.66)
, (1.66) . (1.67)
. (1.67)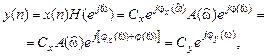 (1.68)
(1.68)
 .
.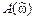 называется частотная зависимость отношения амплитуды реакции к амплитуде дискретного гармонического воздействия в установившемся режиме:
называется частотная зависимость отношения амплитуды реакции к амплитуде дискретного гармонического воздействия в установившемся режиме: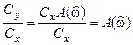 .
. называется частотная зависимость разности фаз реакции и дискретного гармонического воздействия в установившемся режиме:
называется частотная зависимость разности фаз реакции и дискретного гармонического воздействия в установившемся режиме: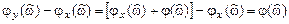 .
.


