Основные свойства частотных характеристик1. ЧХ 2. ЧХ
Доказательство периодичности функций следует из того, что их аргумент
В зависимости от используемой шкалы частот период ЧХ, АЧХ и ФЧХ равен
Если коэффициенты ПФ вещественные (а другие не рассматриваются), то АЧХ будет четной, а ФЧХ – нечетной функцией частоты [1]:
Напомним, что четной называется такая функция, которая не изменяет своего значения при изменении знака переменной. Если же при изменении знака переменной изменяется знак функции, а ее абсолютное значение сохраняется неизменным, то такая функция называется нечетной. На практике представляют интерес графики АЧХ и ФЧХ в основной полосе частот (см. п. 1.1.2).
|
, АЧХ 
и ФЧХ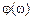 
– непрерывные функции частоты по определению.
.
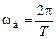– периодическая функция частоты с периодом 
.
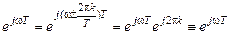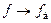; (1.70)
; (1.71)
. (1.72)
;
.
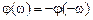