Экспресс-анализ АЧХ и ФЧХ звена 2-го порядка
На практике часто требуется оценить АЧХ и ФЧХ при минимуме расчетов. С этой целью строят приближенные графики рассматриваемых характеристик по их значениям в нескольких точках, количество которых должно быть минимально достаточным. Такой быстрый способ оценки частотных характеристик называется экспресс - анализом. Экспресс-анализ АЧХ предполагает заранее известными особенности анализируемой функции: гладкость, количество экстремумов, нулей и др. Проведем экспресс-анализ АЧХ и ФЧХ звена 2-го порядка. Методами математического анализа можно показать, что в основной полосе частот АЧХ звена 2-го порядка (1.81): - имеет экстремум либо нуль на границах основной полосы, при этом нуль будет наименьшим значением, но не минимумом АЧХ; - может иметь один максимум и один минимум либо нуль внутри основной полосы, при этом нуль будет наименьшим значением, но не минимумом АЧХ. При отсутствии нулей АЧХ представляет собой гладкую функцию. Следовательно, для оценки АЧХ звена 2-го порядка достаточно построить ее график по пяти точкам: - двум – на границах основной полосы, - одной (уточняющей) – посередине основной полосы, - двум – внутри основной полосы, соответствующим максимуму и минимуму (либо нулю) АЧХ. Полагая, что передаточная функция
где
Определим значения АЧХ и ФЧХ в указанных пяти точках: 1) в точке
откуда
Рис. 1.15. Соответствие значений 2) в точке
откуда
Рис. 1.16. Соответствие значений 3) в точке
откуда
Рис. 1.17. Соответствие значений 4) точка
значение АЧХ в этой точке вычисляется по общей формуле (1.81); 5) точка
значение минимума АЧХ в точке если в точке Строго говоря, на местоположение максимума АЧХ влияют не только полюсы, но и нули, так же, как на местоположение минимума АЧХ влияют не только нули, но и полюсы. Тем не менее доминирующее влияние на местоположение максимума оказывают полюсы, а на местоположение минимума – нули, что и отражается символом приблизительного равенства в (1.89)–(1.90) [1].
|

 (1.49) звена 2-го порядка известна, получим формулы экспресс-анализа АЧХ и ФЧХ по следующим пяти точкам
(1.49) звена 2-го порядка известна, получим формулы экспресс-анализа АЧХ и ФЧХ по следующим пяти точкам ,
,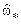 – частота, на которой АЧХ имеет максимум внутри основной полосы (частота максимума АЧХ);
– частота, на которой АЧХ имеет максимум внутри основной полосы (частота максимума АЧХ); – частота, на которой АЧХ имеет минимум или равна нулю внутри основной полосы (частота минимума или нуля АЧХ).
– частота, на которой АЧХ имеет минимум или равна нулю внутри основной полосы (частота минимума или нуля АЧХ).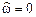 (рис. 1.15)
(рис. 1.15)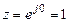 ;
;  ,
,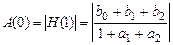 ; (1.83)
; (1.83)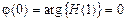 ; (1.84)
; (1.84)
 и
и 
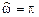 (рис. 1.16)
(рис. 1.16) ;
; 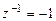 ,
, ; (1.85)
; (1.85) ; (1.86)
; (1.86)
 и
и 
 (рис. 1.17)
(рис. 1.17) ;
;  ,
, ; (1.87)
; (1.87)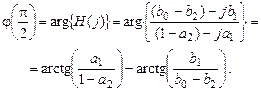 (1.88)
(1.88)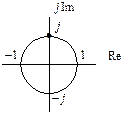
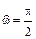 и
и 
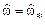 определяет местоположение максимума АЧХ, который находится приблизительно на частоте
определяет местоположение максимума АЧХ, который находится приблизительно на частоте  полюса [1]
полюса [1]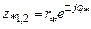 ;
; ; (1.89)
; (1.89)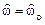 определяет местоположение минимума АЧХ, который находится приблизительно на частоте
определяет местоположение минимума АЧХ, который находится приблизительно на частоте 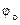 нуля передаточной функции при значении
нуля передаточной функции при значении 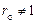 [1]
[1]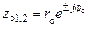 ;
; ,
,  вычисляется по общей формуле (1.81);
вычисляется по общей формуле (1.81); , имеем не минимум, а нуль АЧХ и соответственно скачок ФЧХ на
, имеем не минимум, а нуль АЧХ и соответственно скачок ФЧХ на 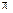 .
.


