Расчет погрешности при косвенных измерениях
Пусть в результате обработки всех непосредственно измеряемых величин x, у, z, … для каждой из них найдены средние значения á x ñ, á у ñ, á z ñ, …, погрешности абсолютные D x,D у,D z, … и относительные ex, ey, ez, …. Требуется найти среднее значение á f ñ искомой величины, а также абсолютную D f и относительную ef погрешности. Среднее значение á f ñ вычисляют при средних значениях величин x, у, z, …, от которых зависит измеряемая величина f, путем их подстановки в расчетную формулу: á f ñ = f (á x ñ, á y ñ, á z ñ, …). (11) Если прямые измерения величин x, у, z, … выполняются независимо и подвержены только случайным погрешностям, то абсолютная погрешность D f косвенно измеряемой величины f определяется следующим образом:
где частные производные Из формулы (12) следует, что влияние составляющей абсолютной погрешности быстро падает по мере уменьшения этой составляющей. Поэтому при вычислении абсолютной погрешности косвенного измерения целесообразно сначала вычислить все ее составляющие Относительная погрешность косвенно измеряемой величины f вычисляется известным способом:
Затем округляют результаты расчета и записывают окончательный результат измерения в стандартном виде: f = (á f ñ ± D f) ед. изм. с ef = … %. (14) Если искомая величина представляет собой выражение вида f = f (x, y, z) = xaybzc, (15) т. е. не содержит операций сложения и вычитания, причем постоянные a, b, c могут принимать как положительные, так и отрицательные значения, проще сначала найти относительную погрешность ef. Действительно,
Прологарифмируем выражение (15): ln f = a ln x + b ln y + c ln z. (17) Вычисляя частные производные, получим:
Окончательно формула для нахождения относительной погрешности примет вид:
После этого рассчитывают абсолютную погрешность D f по формуле: D f = ef ×á f ñ и записывают окончательный результат в виде формулы (14).
|

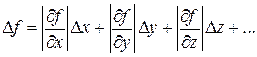 , (12)
, (12)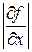 ,
, 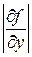 ,
, 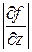 , … вычисляются при средних значениях á x ñ, á у ñ, á z ñ, …, а количество слагаемых в сумме определяется числом величин, абсолютные погрешности которых найдены (подробнее о частных производных см. в прил. 4).
, … вычисляются при средних значениях á x ñ, á у ñ, á z ñ, …, а количество слагаемых в сумме определяется числом величин, абсолютные погрешности которых найдены (подробнее о частных производных см. в прил. 4).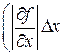 ,
, 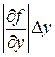 ,
, 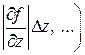 , сравнить их и затем пренебречь теми, которые меньше максимальной в несколько раз. Кроме того, сравнивая значения составляющих погрешностей, можно выявить значение прямого измерения, которое в наибольшей степени влияет на общую погрешность. При необходимости точность результата этого измерения можно увеличить в целях повышения точности эксперимента в целом.
, сравнить их и затем пренебречь теми, которые меньше максимальной в несколько раз. Кроме того, сравнивая значения составляющих погрешностей, можно выявить значение прямого измерения, которое в наибольшей степени влияет на общую погрешность. При необходимости точность результата этого измерения можно увеличить в целях повышения точности эксперимента в целом.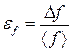 ×100 %. (13)
×100 %. (13)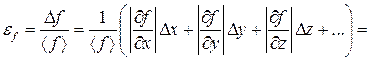
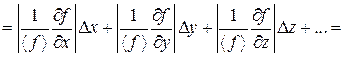
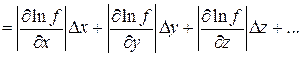 (16)
(16)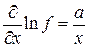 ;
; 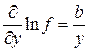 ;
; 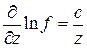 . (18)
. (18)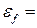
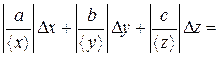 aex + bey + cez. (19)
aex + bey + cez. (19)


