С помощью формул численного дифференцирования
Абсолютную погрешность D f косвенно измеряемой величины f можно определить без непосредственного вычисления частных производных, используя формулы численного дифференцирования (см. прил.5). Полученная на основе выражения (12) формула для нахождения D f примет вид:
Заметим, что
4. пример измерения и расчета погрешности
Цель измерения: определить объем твердого тела, имеющего форму цилиндра. Объем V тела можно измерить непосредственно, погружая тело в мензурку с водой. Однако будем считать, что нет возможности прямыми методами измерить объем тела (нет подходящей мензурки). тогда объем цилиндра вычислим по формуле:
где d и h - диаметр основания и высота цилиндра соответственно. Из формулы (29) видно, что необходимы прямые измерения диаметра d основания и высоты h цилиндра. 1) Проведем прямые измерения. При измерении диаметра d основания цилиндра штангенциркулем с ценой деления в 0,1 мм в пяти различных положениях были получены следующие значения (в мм): 39,6; 39,8; 39,5; 39,6; 39,7. Проведем математическую обработку результатов прямых измерений диаметра d основания цилиндра: а) среднее арифметическое значение диаметра á d ñ = б) абсолютная погрешность многократных измерений диаметра D d = = 0,188 мм» 0,19 мм; (31) в) относительная погрешность измерений ed = (0,19/39,64)×100 % = 0,48 %; г) окончательный результат измерения диаметра цилиндра записывается в виде: d = (39,64 ± 0,19) мм с ed = 0,48 %. (32) Измерения штангенциркулем высоты цилиндра в пяти различных местах в пределах инструментальной погрешности в 0,1 мм не обнаружили непараллельности оснований цилиндра (это указывает на малые случайные погрешности D h cл < D h ин). Результат измерения запишем в виде: h = (52,9 ± 0,1) мм с eh = 0,19 %. (33) Число p = 3,14 ± 0,005 с ep = 0,16 % (в соответствии с прил. 3). 2) Действительное значение объема подсчитаем по формуле (29), подставив в нее средние значения á π;ñ, á d ñ, á h ñ:
3) Абсолютную погрешность D V найдем двумя способами. 1 способ. Используя формулу (12), запишем
Найдем частные производные от V по каждой измеренной величине и подставим их в формулу (35):
Расчет абсолютной погрешности даст результат:
2 способ. В соответствии с формулой (28)
Подставим числовые значения в формулу (38) и получим:
Как видно, вычисленные разными способами значения абсолютной погрешности (37) и (39) с точностью до двух значащих цифр совпадают. С учетом правил округления (см. прил. 2) абсолютная погрешность измерения объема D V = 8,5∙10 –7 м3. (40) 4) Относительная погрешность результата
5) Окончательный результат измерения объема цилиндра с учетом правил округления (см. прил. 2) запишем в виде: V = (6,525 ± 0,085)×10 –5 м3 с eV = 1,3 %. (42)
5. КОНТРОЛЬНЫЕ ПРИМЕРЫ ДЛЯ ЗАЧЕТА
На итоговом занятии по теории погрешностей необходимо выполнить контрольные задания из табл. 3. В каждом задании требуется провести математическую обработку результатов прямых и косвенных измерений (по разрешению преподавателя можно наметить лишь основные этапы расчета, не проводя его). Таблица 3 Контрольные примеры для зачета
Окончание табл.3
6. графическое представление результатов измерений
В процессе измерений часто приходится иметь дело с физическими величинами, находящимися в некоторой функциональной зависимости друг от друга (y = f (x)). В качестве примеров приведем линейную зависимость электрического сопротивления R проводника от температуры: R (t °) = at ° + R 0, квадратичную зависимость пройденного пути s от времени:
Экспериментальные результаты наносятся на координатную плоскость в виде точек. Обычно каждая точка является результатом многократно повторенных измерений. Чтобы отобразить на графике точность, с которой получены результаты, для каждой точки откладываются доверительные интервалы в виде двух взаимно перпендикулярных отрезков, пересекающихся в данной точке. Длина отрезка в выбранном масштабе равна соответствующему доверительному интервалу, например (á x ñ – D x, á x ñ + D x), т. е. удвоенной абсолютной погрешности измерения, а сама точка находится в середине отрезка (см. рисунок). При построении графика рекомендуется провести плавную линию (а не ломаную) так, чтобы она проходила по возможности ближе к экспериментальным точкам в пределах доверительных интервалов. Построить такую плавную линию, которая наилучшим образом выражала бы функциональную зависимость у от х, можно, в частности, при помощи метода наименьших квадратов [5]. Необходимо также учесть, что на чертеже, где кривая идет монотонно, можно ограничиться небольшим числом точек, а вблизи точек максимума, минимума или перегиба измерения производятся чаще и соответственно на графике точки наносятся гуще. Чертят график на миллиметровой бумаге или на бумаге в клетку. Библиографический список 1. Тейлор Дж. Введение в теорию ошибок / Дж. Тейлор: Пер. с англ. М.: Мир, 1985. 272 с. 2. Зайдель А. Н. Погрешности измерений физических величин / А. Н. Зейдель. Л.: Наука, 1985. 112 с. 3. Кассандрова О. Н. Обработка результатов наблюдений / О. Н. Кассандрова, В. В. Лебедев. М.: Наука, 1970. 104 с. 4. Деденко Л. Г. Математическая обработка и оформление результатов эксперимента / Л. Г. Деденко, В. В. Керженцев / МГУ. М., 1977. 112 с. 5. Литневский Л. А. Метод наименьших квадратов в лабораторном практикуме по физике / Л. А. Литневский, С. А. Минабудинова / Омский гос. ун-т путей сообщения. Омск, 2004. 32 с. Приложение 1
|

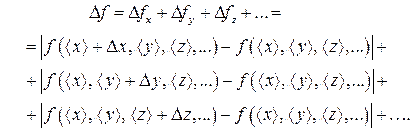 (28)
(28)
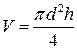 , (29)
, (29) = 39,64 мм; (30)
= 39,64 мм; (30) =
=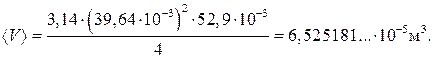 (34)
(34) . (35)
. (35)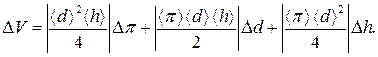 (36)
(36)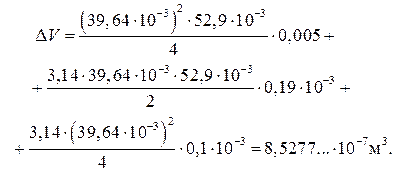 (37)
(37) (38)
(38)
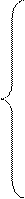 (39)
(39) (41)
(41)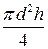
 CU 2
CU 2

 i, мм: 12; 11; 14; 13; 12;
di, мм: 0,30; 0,29; 0,31; 0,32; 0,30
i, мм: 12; 11; 14; 13; 12;
di, мм: 0,30; 0,29; 0,31; 0,32; 0,30
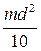
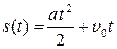 и т. п. Чтобы получить наглядное представление о взаимной связи рассматриваемых величин и их закономерном изменении, результаты измерений следует представлять графически.
и т. п. Чтобы получить наглядное представление о взаимной связи рассматриваемых величин и их закономерном изменении, результаты измерений следует представлять графически.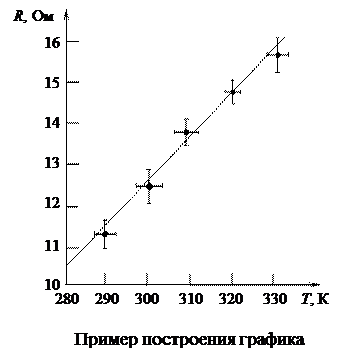 В большинстве случаев пользуются прямоугольной системой координат (см. рисунок). Значения независимой переменной х откладывают по оси абсцисс, а по оси ординат – значения функции у. На координатных осях при этом указываются названия откладываемых величин и единицы их измерения; единицы измерения пишут справа от измеряемых параметров через запятую. Масштаб графика следует выбирать таким образом, чтобы график занимал бóльшую часть координатной плоскости, поэтому за начало отсчета координат необязательно принимать нулевые значения измеренных величин. Если измеренные значения величин заключены в интервалах от х min до x max и от y min до y max, то при нанесении шкал можно начало отсчета совместить со значениями, близкими к х min и y min. Масштабные деления откладывают на координатных осях равномерно через 10 – 20 мм.
В большинстве случаев пользуются прямоугольной системой координат (см. рисунок). Значения независимой переменной х откладывают по оси абсцисс, а по оси ординат – значения функции у. На координатных осях при этом указываются названия откладываемых величин и единицы их измерения; единицы измерения пишут справа от измеряемых параметров через запятую. Масштаб графика следует выбирать таким образом, чтобы график занимал бóльшую часть координатной плоскости, поэтому за начало отсчета координат необязательно принимать нулевые значения измеренных величин. Если измеренные значения величин заключены в интервалах от х min до x max и от y min до y max, то при нанесении шкал можно начало отсчета совместить со значениями, близкими к х min и y min. Масштабные деления откладывают на координатных осях равномерно через 10 – 20 мм.


