Понятие о частных производных
Пусть дана функция нескольких переменных f = f (x, у, z, …). Если зафиксировать значение всех независимых переменных, кроме одной, то f станет функцией этой одной переменной и по ней можно брать производную по известным правилам. Такие производные называются частными. Другими словами,
Символы
однако первые два обозначения из них предпочтительнее. Отметим, что правила вычисления частных производных от конкретных функций совпадают с правилами, применяемыми для функций одной переменной, только требуется каждый раз помнить, по какой переменной берется производная, а к остальным переменным относиться как к постоянным. Примеры. Дана функция нескольких переменных; требуется найти частные производные по всем переменным. 1. f (x, y) = x 2sin y.
2. f = xy.
3. f = x 2 + z 2 + xz3 –
Приложение 5
|

 – частная производная по переменной х от функции f,
– частная производная по переменной х от функции f,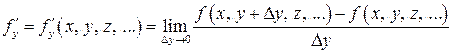 – частная производная по переменной у от функции f,
– частная производная по переменной у от функции f,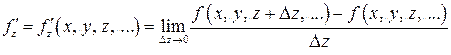 – частная производная по переменной z от функции f и т. п.
– частная производная по переменной z от функции f и т. п.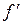 или
или 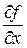 ;
; 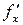 ;
; 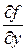 = x 2соs y (здесь х рассматривается как постоянная).
= x 2соs y (здесь х рассматривается как постоянная). .
. (здесь х и z рассматриваются как постоянные);
(здесь х и z рассматриваются как постоянные);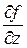 = 2 z + 3 xz 2 –
= 2 z + 3 xz 2 – 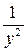 (здесь х и y рассматриваются как постоянные).
(здесь х и y рассматриваются как постоянные).


