Численное дифференцирование
Пусть дана функция f = f (x). Производная функции
Приближенное значение производной
В том случае, когда дана функция нескольких переменных f = f (x, у, z, …), подобным образом вычисляются частные производные:
Учебное издание
КРОХИН Сергей Николаевич, ЛИТНЕВСКИЙ Леонид Аркадьевич, МИНАБУДИНОВА Сания Анасовна
Измерения и расчет погрешностей в лабораторном практикуме по физике _________________
Редактор Т. С. Паршикова
* * *
Подписано в печать.. 2011. Формат 60´84 1/16. Плоская печать. Бумага офсетная. Усл. печ. л.,. Уч.-изд. л.,. Тираж 1000 экз. Заказ.
* *
Редакционно-издательский отдел ОмГУПСа Типография ОмГУПСа
*
644046, г. Омск, пр. Маркса, 35
С. Н. Крохин, Л. А. Литневский, С. А. Минабудинова
ИЗМЕРЕНИЯ И РАСЧЕТ ПОГРЕШНОСТей в лабораторном практикуме по физике
|
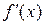в точке x в соответствии с определением задается следующим выражением: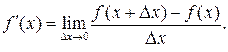
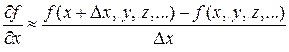– частная производная по переменной х от функции f,
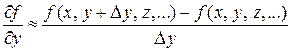– частная производная по переменной y от функции f,
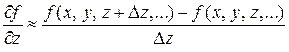– частная производная по переменной z от функции f и т.п.
Омск 2011
