Условие сходимости метода. Понятие сжимающего отображения.
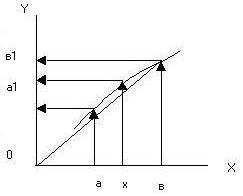
Решить вопрос о сходимости метода можно с помощью понятия сжимающее отображение. Доказательство: Возьмем непрерывную функцию φ(х) заданную на некотором отрезке [a;b]. Каждой точке x из отрезка [a;b] соответствует некоторое значение y = φ(х) на оси ординат. Т.е. функция отрезка [a;b] задает отображение на оси ординат. Чтобы сравнить образ отрезка с ним самим отобразим отобразить точки на оси 0y через симметрично относительно прямой y=x. Если образ отрезка [a;b] является частью [a;b], то j(x) отображает [a;b] в себя. Будем продолжать этот процесс бесконечно и полечим последовательность отрезков. Если после каждого отображения отрезок уменьшается в М>1 раз, то отображение называется сжимающим и можно записать следующее | φ(a)-φ(b)|≤q|a-b|, q=1/M.
|
Теорема: Пусть в некоторой δ - окрестности корня х* функция φ(х) дифференцируема и удовлетворяет неравенству |φ'(x)|≤ q, 0 < q < 1. Тогда независимо от выбора начального приближения х0 из указанной δ - окрестности корня итерационная последовательность не выходит из этой окрестности и справедлива следующая оценка сходимости: |xk-x*|<q|x0-xk| что говорит о линейной скорости сходимости.
