Решение нелинейного уравнения методом простых итераций. Понятие сжимающего отображения. Теорема о сходимости. Геометрическая интерпретация.
Основные понятия вычислительной математики.
Для решения математических задач применяется 3 группы методов: аналитические, графические, численные. Графические методы предполагают искать решение с помощью геометрических построений. Аналитические методы предполагают искать решение задачи в виде формулы. Численные методы являются основными методами в САПР. В их основе лежит процедура сведения решения задачи к конечному числу арифметических действий над числами, и получить результат в виде численных значений. Основные требования и показатели численных методов является устойчивость, точность, сходимость, эффективность (скорость сходимости). Алгоритм считается устойчивым, если он обеспечивает нахождение существующего и единственного решения при различных исходных данных.
Скорость сходимости выражается в количестве шагов, которое метод затрачивает для поиска решения. Алгоритм обладает линейной скоростью сходимости, если a<q<b, |xk-1-x*|≤q|xk-x*|. Алгоритм обладает сверхлинейной скоростью сходимости, если выполняется условие |xk+1-x*|£qk |xk-x*|, q ®0, k ® ¥;. Алгоритм обладает квадратичной скоростью сходимости, если |xk+1-x*|£q|xk-x*|2.
Решение нелинейного уравнения методом простых итераций. Понятие сжимающего отображения. Теорема о сходимости. Геометрическая интерпретация.
|

 Применение ВТ базируется на описании процессов реального мира мат. модели, которая представляет собой совокупность обычных интегральных и дифференциальных уравнений. Всякая математическая модель представляет собой математическое преобразование вида «черный ящик», где x(x1..xn) вектор входных параметров объектов, y(y1..ym) вектор управлений воздействий на объект, U(U1..Uk) совокупность выходных параметров объектов и F - оператор преобразования.
Применение ВТ базируется на описании процессов реального мира мат. модели, которая представляет собой совокупность обычных интегральных и дифференциальных уравнений. Всякая математическая модель представляет собой математическое преобразование вида «черный ящик», где x(x1..xn) вектор входных параметров объектов, y(y1..ym) вектор управлений воздействий на объект, U(U1..Uk) совокупность выходных параметров объектов и F - оператор преобразования.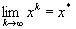 Сходимость является основным критерием оценки алгоритма. Алгоритм сходится, если итерационная последовательность приближений x1,x2,...,xk® x*, k ® ¥, т. е.
Сходимость является основным критерием оценки алгоритма. Алгоритм сходится, если итерационная последовательность приближений x1,x2,...,xk® x*, k ® ¥, т. е.


