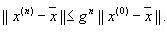Сходимость метода. Пусть j'(x) - матрица Якоби, соответствующая функции j(x).
Пусть j'(x) - матрица Якоби, соответствующая функции j(x). Теорема. Пусть в некоторой s - окрестности решения x¯ функции ji(x) непрерывно дифференцируемы и выполнено неравенство ||j'(x)||£g, где 0£ g<1. Тогда независимо от выбора начального приближения x(0) из указанной s-окрестности корня итерационная последовательность не выходит из этой окрестности, метод сходится со скоростью геометрической прогрессии и справедлива следующая оценка погрешности:
На практике часто используется следующая оценка окончания итерационного процесса: ||x(n)-x(n-1)||£e
|