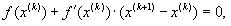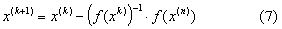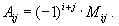Метод Ньютона.
Обобщим метод Ньютона для решения одного НУ на решение системы НУ (1). Заменим в системе (1) каждую функцию fi (х) линейной частью ее разложения в ряд Тейлора в точке x(n):
где f - матрица Якоби.
Тогда система (6) имеет единственное решение, которое принимается за очередное приближение x(k+1) к решению x, то есть приближение x(k+1) удовлетворяет равенству выразив из полученного равенства x(k+1), получим формулу метода Ньютона:
где Aij - алгебраическое дополнение элемента aij.
Mij - минор элемента aij, то есть определитель порядка n - 1, получающийся из A вычеркиванием i - ой строки и j - го столбца.
|
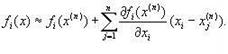
В результате данного преобразования перейдем к СЛАУ имеющей в матричной форме следующий вид:
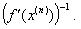Предположим, что матрица Якоби невырожденная, то есть существует обратная матрица
