Интерполяционный многочлен Лагранжа. Теорема о единственности.
Перейдем к случаю глобальной интерполяции, то есть построению интерполяционного многочлена, единого для всего отрезка [x0, xn]. При этом график интерполяционного многочлена должен проходить через все заданные точки. Запишем искомый многочлен в виде:
Из условий равенства значений этого многочлена в узлах xi соответствующим заданным табличным значениям yi, получим систему уравнений для нахождения коэффициентов a0, a1,...,an:
Рассмотрим более простой алгоритм построения интерполяционных алгоритмов. Будем искать многочлен в виде линейной комбинации множеств степени n.
Потребуем, чтобы каждый многочлен
Подставив эти формулы в исходный многочлен получим:
Эта формула называется интерполяционным многочленом Лагранжа. Докажем, что этот многочлен является единственным. Допустим противоположное: пусть существует еще один многочлен F(x) степени n, принимающий в узлах интерполяции значения табличной функции, то есть F(xi) = yi, i = 0,n. Но не совпадающий с L(x). Так как F(xi) = yi и L(xi) = yi, то разность R(x) = L(x) - F(x), являющаяся многочленом степени не более n в узлах xi =0
Если R(x)=L(x)-F(x) ≠ 0, то разность R(x) (будучи многочленом не выше n-й степени- это следует из вида многочлена L(x), в котором n+1 слагаемое, каждое по n множителей), в силу основной теоремы высшей алгебры имеет n корней. Это противоречит виду R(x). [ Основная теорема алгебры: каждое алгебраическое уравнение n-й степени
коэффициенты, которого a1,a2,...,an - действительные или комплексные числа, имеет ровно n корней действительных или комплексных.] Это противоречит равенствам:
Возникло противоречие: многочлен, который не может иметь более n корней, имеет n+1 корень. Следовательно, многочлены L(x) и F(x) тождественны (L(x) F(x)). Из формулы интерполяционного многочлена Лагранжа
|

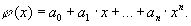
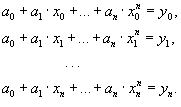 Решив эту систему, найдем коэффициенты интерполяционного многочлена. Заметим, что такой путь построения многочлена может потребовать больших вычислений, особенно при большом числе узлов.
Решив эту систему, найдем коэффициенты интерполяционного многочлена. Заметим, что такой путь построения многочлена может потребовать больших вычислений, особенно при большом числе узлов.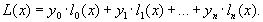
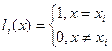 таким условиям отвечает многочлен вида:
таким условиям отвечает многочлен вида: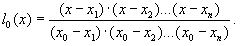
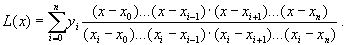
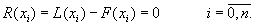
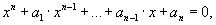
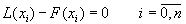 число, которых равно n + 1 (система из (n+1)-го уравнения).
число, которых равно n + 1 (система из (n+1)-го уравнения).


