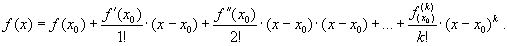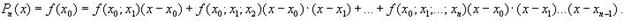Свойства разделенных разностей.
1) разделительная разность f(xi; xi+1;xi+k) является симметричной функцией своих аргументов xi,xi+1,xi+k (не изменяется относительно любой их перестановки); 2) пусть функция f(x) на отрезке [a;b], содержащем точки xi,xi+1,xi+k, имеет производную порядка k. В этом случае:
Любая функция, непрерывная на [a;b] и имеющая на этом отрезке производные, включая k-ю, может быть разложена в ряд Тейлора:
Используя свойства распределенных разностей запишем интерполяционный многочлен Ньютона с распределенными разностями:
|